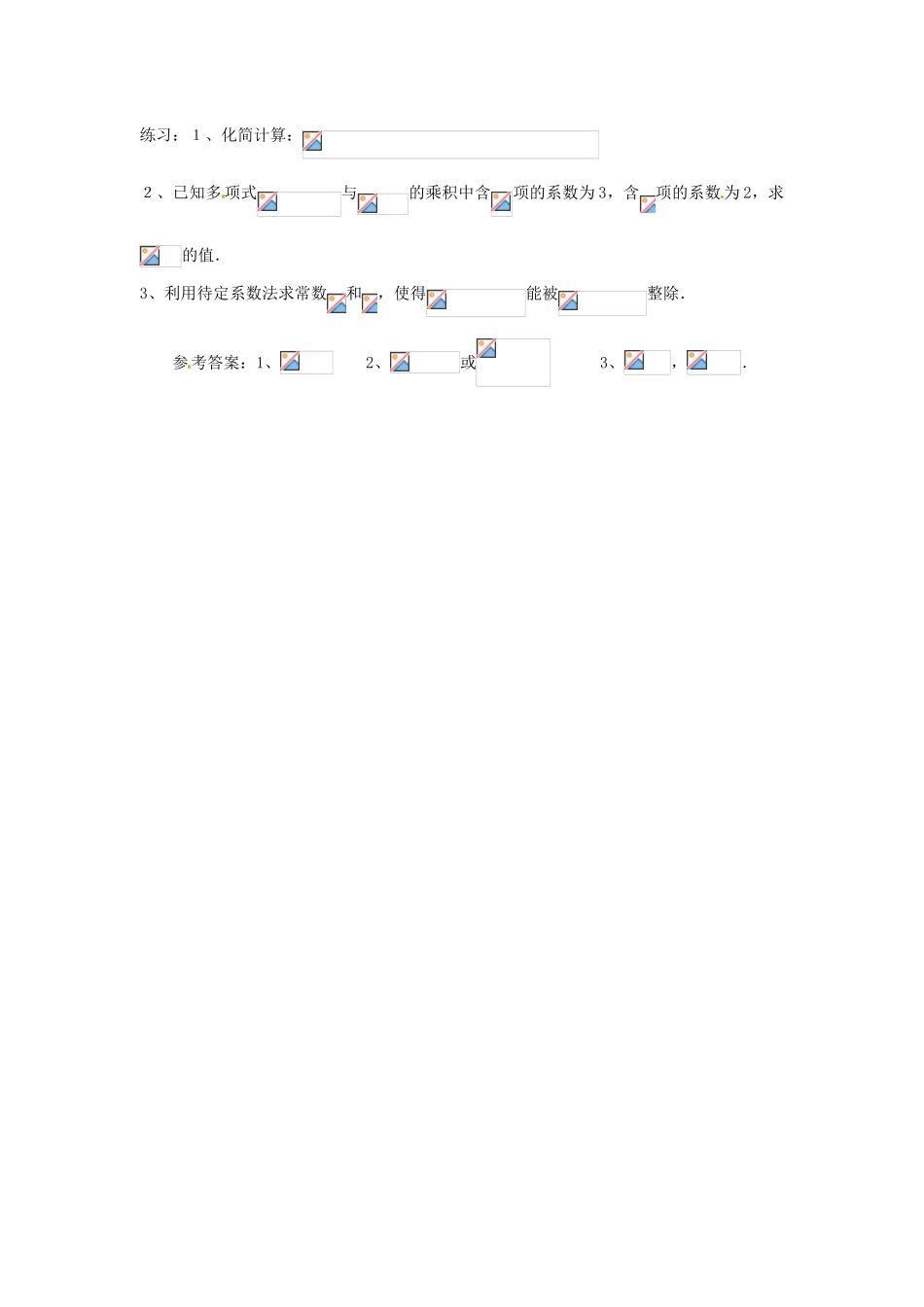
巧用乘法公式妙解题教案一、利用整式乘法进行计算⑵、化简:解:原式=.评析:这两个题目表面看是关于数的计算,显然直接计算是非常困难的.从以上的解题方法我们可以看出,利用整式乘法的数学思想进行计算,非常容易的得到答案.这正是数学的魅力.二、利用条件表示已知的代数式或求值⑶、已知:,,.用含有m、n、p的式子表示.解:⑷、设,.求的值.解:∵,∴,又,∴.∵,而,∴,即评析:这两个题目一个是用字母表示代数式,一个是用数字表示代数式,也就是求代数式式的值.在这些变化中,体现了整式乘法的灵活运用,从而使数学计算变得简单有趣、生动活波.三、求待定的字母或代数式的值⑸已知多项式的乘积展开后不含和项,求和的值.解:由于,∵展开后不含和项,∴,解得.评析:这两个题目的思路是一样的,主要方法是比较等式两边对应项的系数.其目的就是要利用等式两边对应项的系数相等这些条件列方程,从而求得相关的字母或代数式的值.四、证明整除性问题⑺试证:对于任意自然数,代数式的值,都能够被6整除.证明:由于∵为自然数,∴必为整数.因此能够被6整除.评析:关于整除性问题,一般来说总是利用整式乘法进行代数式的变换,找出所含有的数字因数或字母因数以及代数式因数,然后就可以确定能否被某数或某式整除.做此类题目也是离不开整式乘法的.练习:1、化简计算:2、已知多项式与的乘积中含项的系数为3,含项的系数为2,求的值.3、利用待定系数法求常数和,使得能被整除.参考答案:1、2、或3、,.