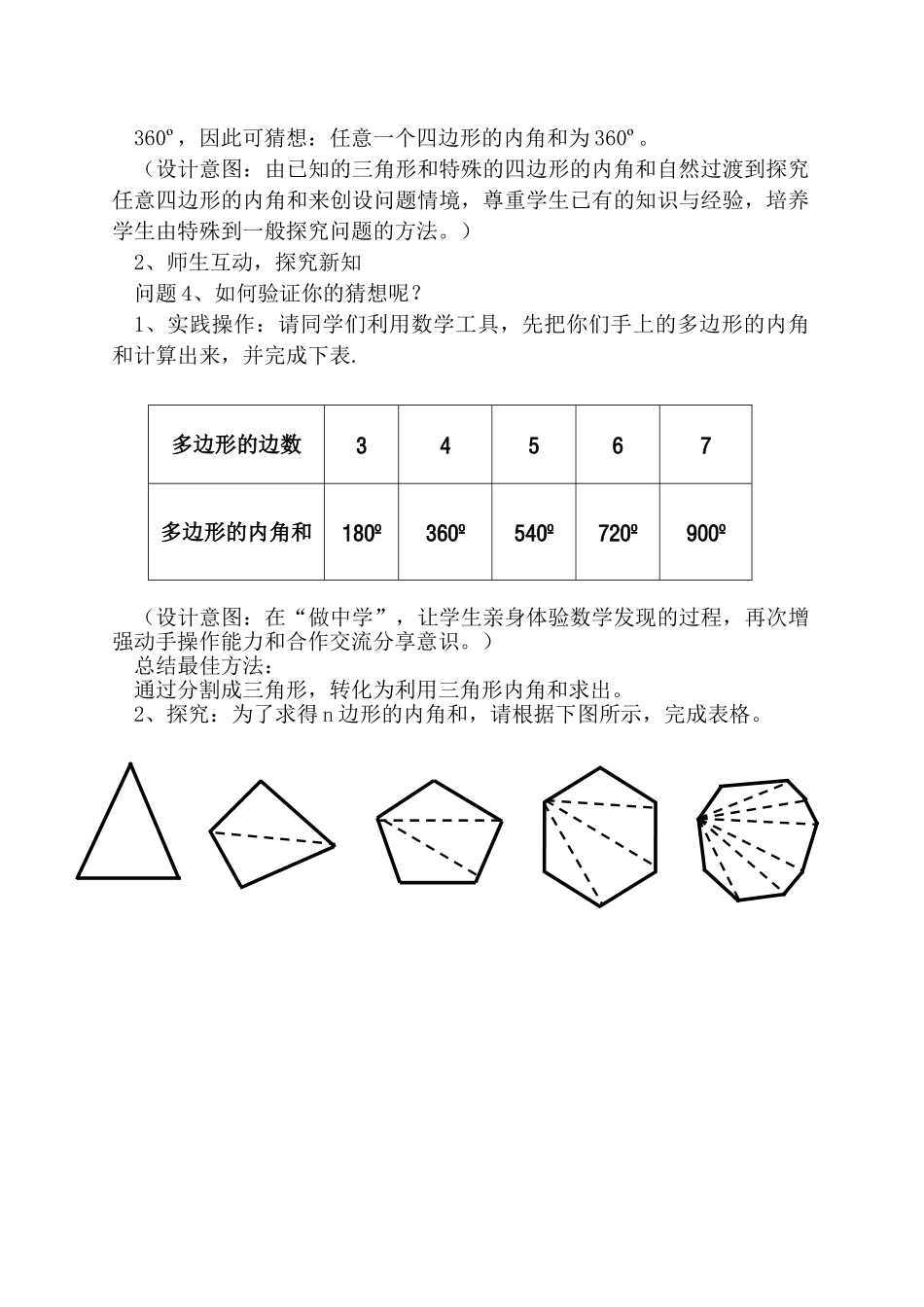
课题:多边形的内角和(第1课时)一、教学目标1.知识目标掌握多边形的内角和公式及其运用。2.能力目标通过引导学生自主探究多边形内角和公式,培养学生探究问题的方法与能力;让学生尝试从不同角度寻求探究问题的方法并能有效的解决问题,训练学生的发散性思维和培养他们的创新精神。3.情感目标通过实例引入,使学生体验数学来源于生活,又服务于生活,唤起学生学数学的兴趣和应用数学的意识。在自主探究、合作交流的过程中,感受数学活动的重要意义和合作成功的喜悦,提高学生学习的热情和合作意识。二、重点和难点重点:多边形的内角和公式的探索以及运用公式进行有关计算。难点:如何引导学生参与到探索多边形的内角和公式的过程。三、教学过程1、情境创设,激发求知欲多媒体投影:(1)好漂亮的图形,由这图形你能抽象出什么几何图形?(2)我们可以利用多边形设计一些美丽的图案。师:这里其实涉及到多边形内角和以及拼图的问题,为了掌握其中的道理,今天我们首先研究多边形的内角和。引入课题,教师板书。(设计意图:让学生感受数学来源于生活并应用于生活以及发现生活中数学的美,达到激趣。最后设疑,达到生疑与欲质疑,自然引入探求新知)问题1、三角形的内角和等于多少度?如何得到此公式?生:180º;通过测量或剪拼发现三角形的三个内角和为180º或刚好组拼成一个平角,由此可想到通过作平行线把三角形的三个内角平移组合成平角或两直线平行同旁内角互补的方法得于验证。```问题2、教室中有四边形的物体吗?是怎样的四边形?内角和分别是多少度?问题3、猜一猜:任意一个四边形的内角和可能是多少度?生:因为任意三角形的内角和为180º,而长方形和正方形的内角和为360º,因此可猜想:任意一个四边形的内角和为360º。(设计意图:由已知的三角形和特殊的四边形的内角和自然过渡到探究任意四边形的内角和来创设问题情境,尊重学生已有的知识与经验,培养学生由特殊到一般探究问题的方法。)2、师生互动,探究新知问题4、如何验证你的猜想呢?1、实践操作:请同学们利用数学工具,先把你们手上的多边形的内角和计算出来,并完成下表.多边形的边数34567多边形的内角和180º360º540º720º900º(设计意图:在“做中学”,让学生亲身体验数学发现的过程,再次增强动手操作能力和合作交流分享意识。)总结最佳方法:通过分割成三角形,转化为利用三角形内角和求出。2、探究:为了求得n边形的内角和,请根据下图所示,完成表格。问题5、你能归纳出n边形的内角和公式了吗?生:n边形的内角和等于(n-2)•180º。(设计意图:形成公式以及培养学生的归纳能力。)问题6、探索多边形的内角和关键是:把多边形分成几个三角形,再利用三角形的内角和求得。你还有其它的分法吗?n×180º-360º(n-1)×180º-180º问题7、同学们对此公式有疑问吗?教师可视学生回答情况给予如下提示:n可以是1或1/3吗?(n-2)表示什么?3、范例教学例1:八边形的内角和是;例2:已知多边形的每一内角为150°,求这个多边形的边数.解:设这个多边形的边数为n,根据题意得(n-2)×180°=150°n解这个方程,得n=12经检验,符合题意答:这个多边形的边数为12.4、课堂测试初步应用,巩固新知(抢答)1、n边形从一个顶点所画对角线的条数是;2、n边形内角和=;3、九边形的内角和是__________4、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为;5、一个多边形的边数增加1,则内角和增加的度数是()A.60°B.90°C.180°D.360°探究如图:某居民小区搞绿化,分别在三角形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积,再根据面多边形的边数3456…n分成的三角形个数1234…n-2多边形的内角和180º360º540º720º…(n-2)×180º积买花苗。你能帮绿化组长求出花坛的面积?(结果保留π)5、课堂小结1、n边形的内角和等于:(n-2)×180°2、方程的数学思想在几何中有重要的作用。3、利用类比归纳、转化的学习方法,可以把多边形问题转化为三角形问题来解决;6、作业A组:课本P62:5、6、7B组:已知一个多边形除了一个内角外,其余...