九年级数学下 锐角三角函数1人教版VIP免费

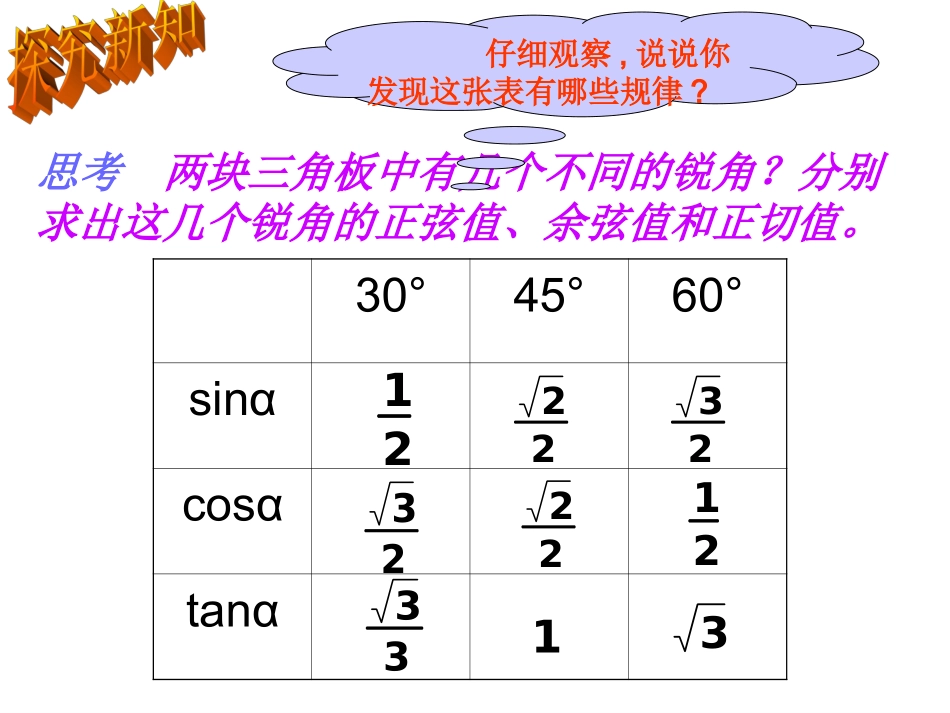
锐角三角函数（3）ABC∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边思考两块三角板中有几个不同的锐角？分别求出这几个锐角的正弦值、余弦值和正切值。30°45°60°sinαcosαtanα1222323222123313仔细观察,说说你发现这张表有哪些规律?1、你能得出互为余角的两个锐角A、B正切值的关系吗?2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?2123222123223313观察与思考仔细观察右表，回答下面问题。例例11、求下列各式的值、求下列各式的值..(2)cos45sin45-tan45(1)cos(1)cos2260°+sin60°+sin2260°60°Cos²60°表示（cos60°）²，即（cos60°）×（cos60°）解：（1）cos²60°+sin²60°=（）²+（）²1232（2）=÷222245tan45sin45cos-1=0.=1；当A、B为锐角时，若A≠B，则sinA≠sinB，cosA≠cosB，tanA≠tanB.操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30度，并已知目高为1.65米．然后他很快就算出旗杆的高度了。1.65米10米?你想知道小明怎样算出的吗？应用生活30°例例33、、(1)(1)如图，在如图，在RtABC△RtABC△中，∠中，∠CC=90°=90°，，AB=,BC=AB=,BC=。求∠。求∠AA的度数。的度数。(2)(2)如图如图,,已知圆锥的高已知圆锥的高AOAO等于圆锥的底面等于圆锥的底面半径半径OBOB的倍的倍,,求求α.α.63363CAB(1)OBA(2)1¡sin230+tan245+sin260cos245+tan30cos3022、已知：、已知：αα为锐角，为锐角，且满足且满足，，求求αα的度数。的度数。3tan2-4tan+3=03、在在RtABC△RtABC△中，∠中，∠C=90°C=90°，化简，化简1-2sinAcosA、