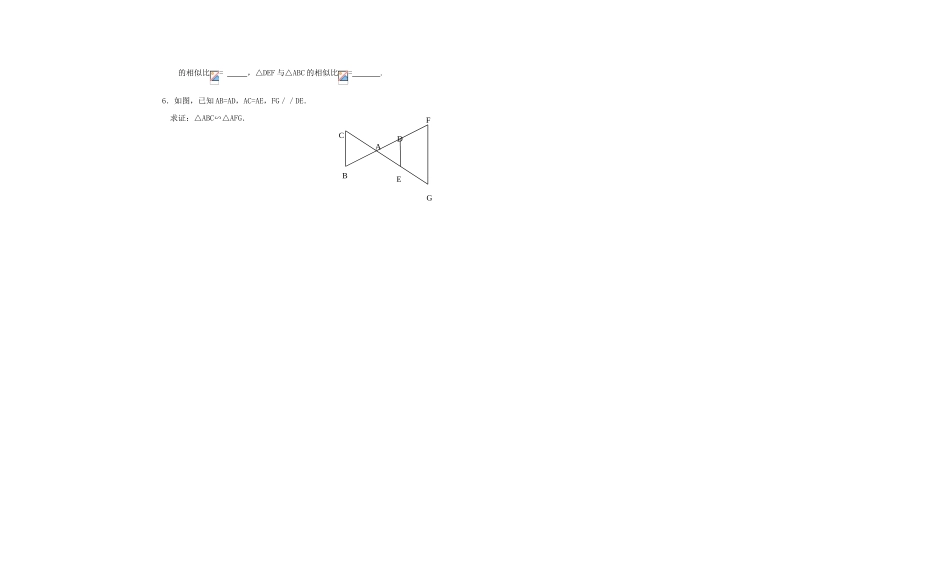
27.2.1相似三角形的判定(一)教学要点:了解相似比的定义,掌握判定两个三角形相似的方法:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;提出问题:如图27·2-1,在∆ABC中,点D是边AB的中点,DE∥BC,DE交AC于点E,∆ADE与∆ABC有什么关系?分析:观察27·2-1易知AD=,AE=,∠A=∠A,∠ADE=∠ABC,∠AED=∠ACB,只需引导学生证得DE=即可,学生不难想到过E作EF∥AB。↓∆ADE∽∆ABC,相似比为。延伸问题:改变点D在AB上的位置,先让学生猜想∆ADE与∆ABC仍相似,然后再用几何画板演示验证。↓归纳:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似探究方法:探究1在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?分析:学生通过度量,不难发现这两个三角形的对应角都相等,根据相似三角形的定义,这两个三角形相似。(学生小组交流)在学生小组交流的基础上引导学生思考证明探究所得结论的途径。练习:1.如图,△ABC中,DE//BC,DF//AC,则图中相似三角形的组数为A.1B.2C.3D.42.已知:△ABC∽△A1B1C1,AC=3,A1C1=1.8,则△与△ABC的相似比为。3.若D、E分别在△ABC的边BC、AC上,CD=BC,CE=AC,则DE∥,△CDE∽.4.已知:梯形ABCD中,AD//BC,且AC、BD相交于点O,过O作EF//AD分别交AB、CD于E、F,则图中共有相似三角形的对数为()A.5对B.4对C.3对D.2对5.已知△ABC∽△DEF,AB:DE=1:3,则△ABC与△DEF的相似比=,△DEF与△ABC的相似比=.6.如图,已知AB=AD,AC=AE,FG//DE.求证:△ABC∽△AFG.BAGFCED