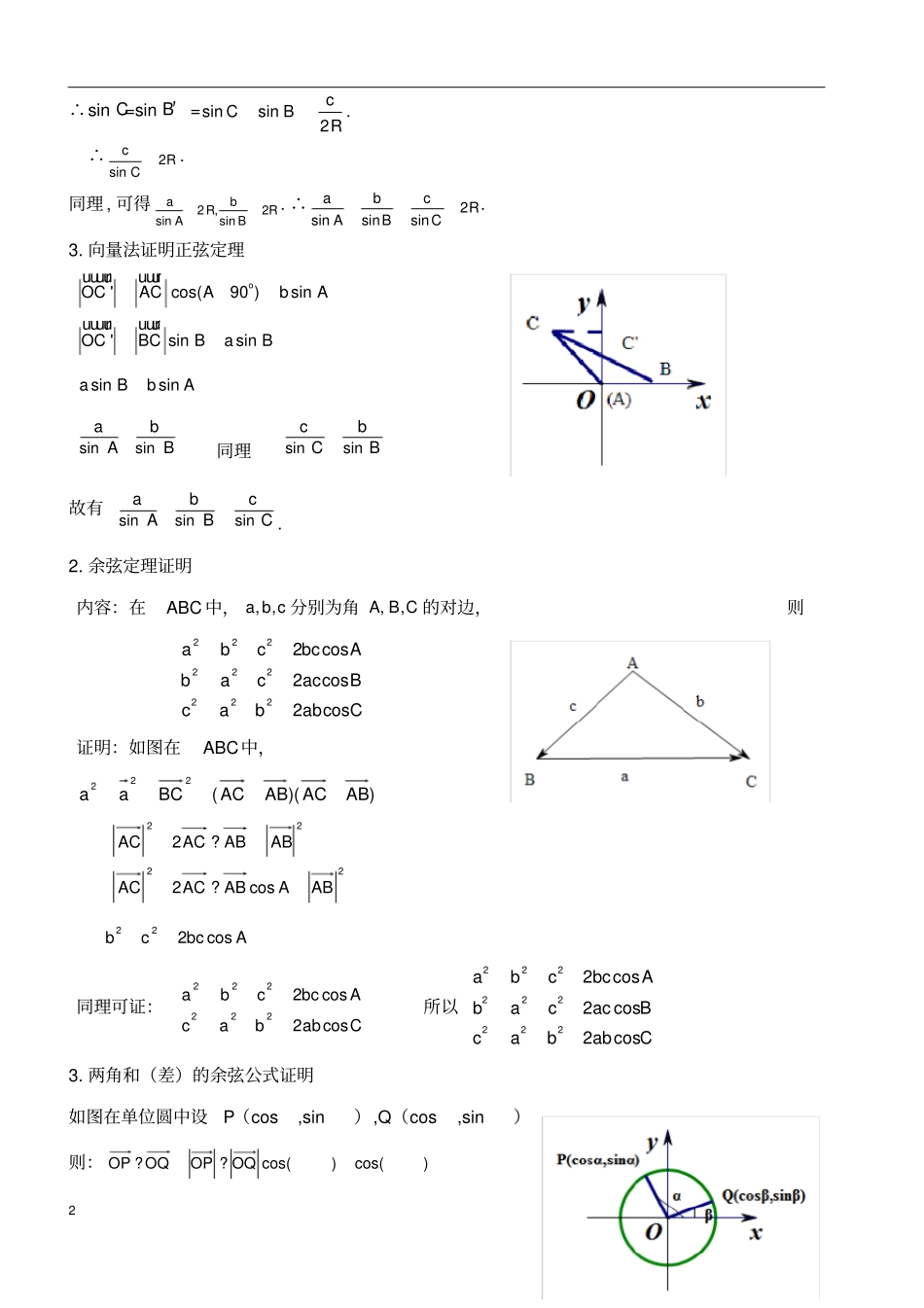
1高中数学相关定理、公式及结论证明一、三角函数部分1.正弦定理证明内容:在ABC中,cba,,分别为角CBA,,的对边,则.sinsinsinCcBbAa证明:1.利用三角形的高证明正弦定理(1)当ABC是锐角三角形时,设边AB上的高是CD,根据锐角三角函数的定义,有sinCDbAsinCDaB。由此,得sinsinabAB,同理可得sinsincbCB,故有sinsinabABsincC.从而这个结论在锐角三角形中成立.(2)当ABC是钝角三角形时,过点C作AB边上的高,交AB的延长线于点D,根据锐角三角函数的定义,有sinsinCDaCBDaABC,sinCDbA。由此,得sinsinabAABC,同理可得sinsincbCABC故有sinsinabAABCsincC.(3)在ABCRt中,,sin,sincbBcaAcBbAasinsin,.1sin,90CC.sinsinsinCcBbAa由(1)(2)(3)可知,在ABC中,sinsinabABsincC成立.2.外接圆证明正弦定理在△ABC中,已知BC=a,AC=b,AB=c,作△ABC的外接圆,O为圆心,连结BO并延长交圆于B′,设BB′=2R.则根据直径所对的圆周角是直角以及同弧所对的圆周角相等可以得到∠BAB′=90°,∠C=∠B′,abDABCABCDba2∴sinC=sinB′=RcBC2sinsin.∴RCc2sin.同理,可得RBbRAa2sin,2sin.∴RCcBbAa2sinsinsin.3.向量法证明正弦定理'cos(90)sinOCACAbAouuuuruuur'sinsinOCBCBaBuuuuruuursinsinaBbAsinsinabAB同理sinsincbCB故有sinsinabABsincC.2.余弦定理证明内容:在ABC中,cba,,分别为角CBA,,的对边,则CabbacBaccabAbccbacos2cos2cos2222222222证明:如图在ABC中,))((222ABACABACBCaa2222cos22ABAABACACABABACAC??Abccbcos222同理可证:CabbacAbccbacos2cos2222222所以CabbacBaccabAbccbacos2cos2cos22222222223.两角和(差)的余弦公式证明如图在单位圆中设P(cos,sin),Q(cos,sin)则:)cos()cos(??OQOPOQOP3sinsincoscos?OQOP)cos(sinsincoscos在单位圆中设P(cos,sin),Q(cos,-sin)则:)cos()cos(??OQOPOQOPsinsincoscos?OQOP)cos(sinsincoscos(或)cos()cos()4.两角和(差)的正弦公式证明二、两角和(差)的正弦公式证明。内容:sincoscossin)sin(,sincoscossin)sin(证明:sin)2sin(cos)2cos(])2cos[()](2cos[)sin(sincoscossinsin)2sin(cos)2cos(])2cos[()](2cos[)sin(sincoscossin5.两角和(差)的正切公式证明内容:tantan1tantan)tan(,tantan1tantan)tan(证明:coscossinsincoscoscoscoscoscossincoscoscoscossinsinsincoscossincoscossin)cos()sin()tan(tantan1tantancoscossinsincoscoscoscoscoscossincoscoscoscossinsinsincoscossincoscossin)cos()sin()tan(tantan1tantan4xyP(x,y)P′(x,-y)MO(4-5-2)180xyP(x,y)P′(-x,-y)MM′O(4-5-1)6.半角公式证明内容:sin2cos1cos1sin2cos1cos12tan,2cos12cos,2cos12sin证明:由二倍角公式1cos22cossin212cos22用代替2,得12cos2cos2sin21cos22,得2cos12cos,2cos12sin??2cos22cos2cos22sin2cos2sin2tancos1sin2,??2sin22cos2sin22sin2cos2sin2tansin2cos17.诱导公式公式:如图:设的终边与单位圆(半径为单位长度1的园)交于点P(x,y),则角-的终边与单位圆的交点必为P′(x,-y).由正弦函数、余弦函数的定义,即可得sin=y,cos=x,sin(-)=-y,cos(-)=x,所以:sin(-)=-sin,cos(-)=cosα由倒数关系和商数关系可以得到有关正切的-诱导公式。公式:-sinsin()-coscos()tantan()它刻画了角180o+与角的正弦值(或余弦值)之间的关系,这个关系是:以角终边的反向延长线为终边的角的正弦值(或余弦值)与角的正弦值(或圆交于点P(x,y),则角终边的反向延长线,即coscos()tantan()-sinsin()5180o+角的终边与单位圆的交点必为P′(-x,-y)(如图4-5-1).由正弦函数、余弦函数的定义,即可得sin=y,cos=x,sin(180o+)=-y,cos(180o+)=-x,所以:sin(180o+)=-sin,cos(180o+)=-cos.由倒数关系和商数关系可以得到有关正切的诱导公式。相应诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαk∈zcos(2kπ+α)=cosαk∈ztan(2kπ+α)=tanαk∈z公式二:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanα公式三:sin(-α)=-sinα公式四:利用公式二和公式三可以得到π-α与α的三角函数值...