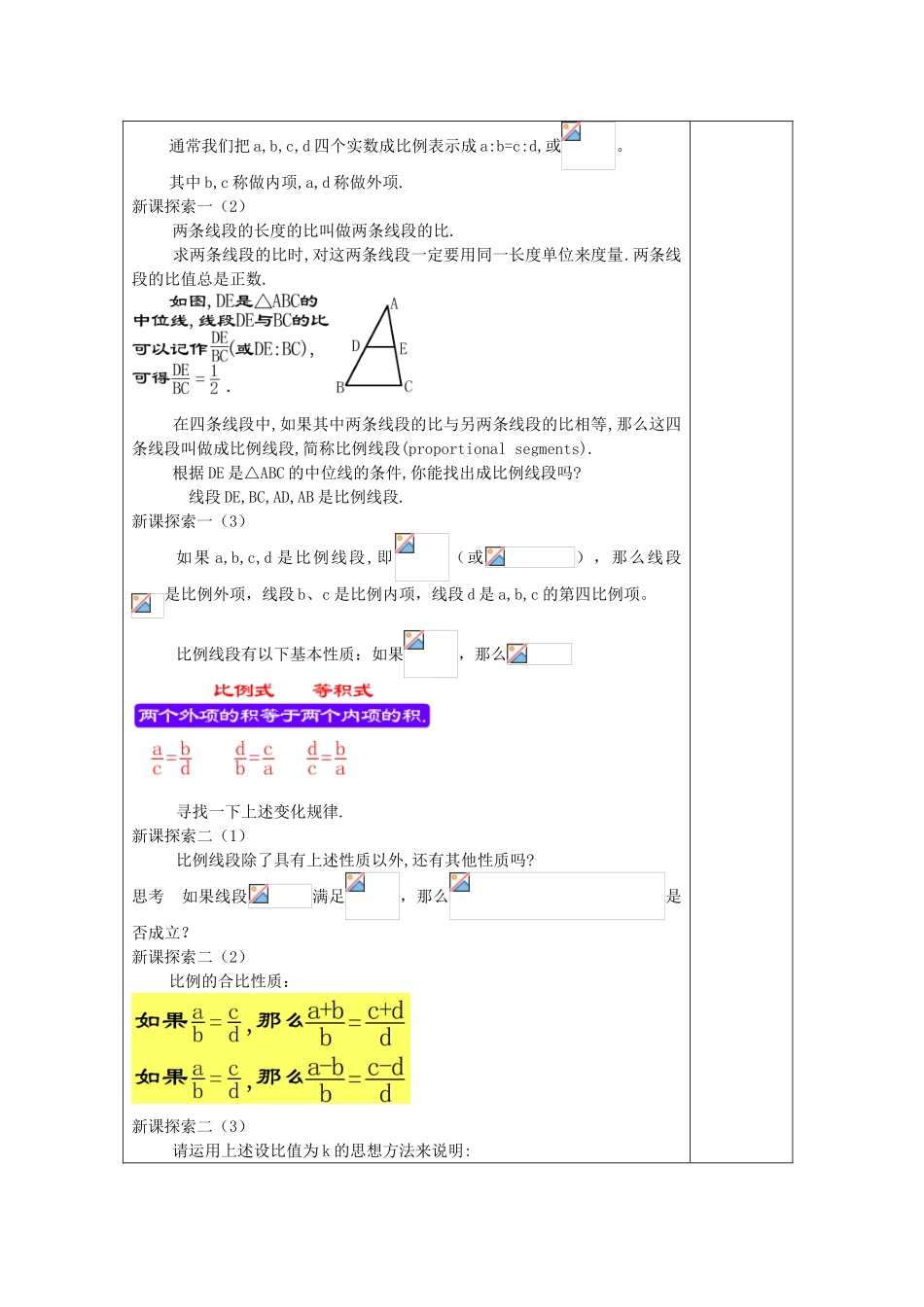
比例线段课题24.2(1)比例线段课型新授课教学目标1.1.知道两条线段比的意义知道两条线段比的意义..2.2.理解比例线段及其有关概念理解比例线段及其有关概念..3.3.知道比例线段的性质知道比例线段的性质..4.4.掌握合比和等比性质掌握合比和等比性质,,能结合具体图形进行简单的比例线段变形能结合具体图形进行简单的比例线段变形..重点比例线段的概念及它的初步应用比例线段的概念及它的初步应用难点合比、等比性质的运用合比、等比性质的运用教学准备比例、比值、成比例学生活动形式讲练结合教学过程课题引入:课前练习一屋架跨度的一半OP长为5米,高度OQ为2.25米,现要在屋顶上开一个天窗,其高度AC为1.2米,AB在水平位置,你能求出AB的长度吗?图形的相似与线段长度的比及比例有密切关联.为了研究相似形,需要先研究比例线段.课前练习二根据下列条件,求a与b的比值:(1)a=10,b=8;(2)a=0.36,b=0.8;(3)a=5千克,b=250千克;(4)a=30厘米,b=2米.备注:情景引入,不需求解.1.复习求比值,注意单位的统一.(六年级上)2.学生练习,教师讲评.以旧引新,由复习比引入比例.知识呈现:新课探索一(1)思考四个数a,b,c,d,若,请问在什么情况下,就说这四个数成比例?k1=k2时,就说这四个数成比例.如果两个数的比值与另两个数的比值相等,就说这四个数成比例.通常我们把a,b,c,d四个实数成比例表示成a:b=c:d,或。其中b,c称做内项,a,d称做外项.新课探索一(2)两条线段的长度的比叫做两条线段的比.求两条线段的比时,对这两条线段一定要用同一长度单位来度量.两条线段的比值总是正数.在四条线段中,如果其中两条线段的比与另两条线段的比相等,那么这四条线段叫做成比例线段,简称比例线段(proportionalsegments).根据DE是△ABC的中位线的条件,你能找出成比例线段吗?线段DE,BC,AD,AB是比例线段.新课探索一(3)如果a,b,c,d是比例线段,即(或),那么线段是比例外项,线段b、c是比例内项,线段d是a,b,c的第四比例项。比例线段有以下基本性质:如果,那么寻找一下上述变化规律.新课探索二(1)比例线段除了具有上述性质以外,还有其他性质吗?思考如果线段满足,那么是否成立?新课探索二(2)比例的合比性质:新课探索二(3)请运用上述设比值为k的思想方法来说明:比例的等比性质:等比性质可以推广到任意有限多个相等的比的情形.例如:注意在实数范围内,式中的分母不能为零,如b+d≠0,b1+b2+b3≠0.新课探索三课内练习一1.已知点B在线段AC上,BC=2AB.则课内练习二2.已知:如图,线段BD与CE相交于点A,课内练习三3.已知x:y=5:2,求(x+y):y的值.课内练习四课内练习五5.如图,表示我国台湾省几个城市的位置关系,问基隆市在高雄市的哪一个方向?到高雄市的实际距离是多少?课堂小结:1.1.两条线段比的意义两条线段比的意义.2..2.比例线段及其有关概念比例线段及其有关概念..3.3.比例线段的性质比例线段的性质.4..4.合比和等比性质。合比和等比性质。课外作业练习册预习要求24.2(2)比例线段课堂时间安排教师主导活动时间:分钟学生主体活动时间:分钟教学后记