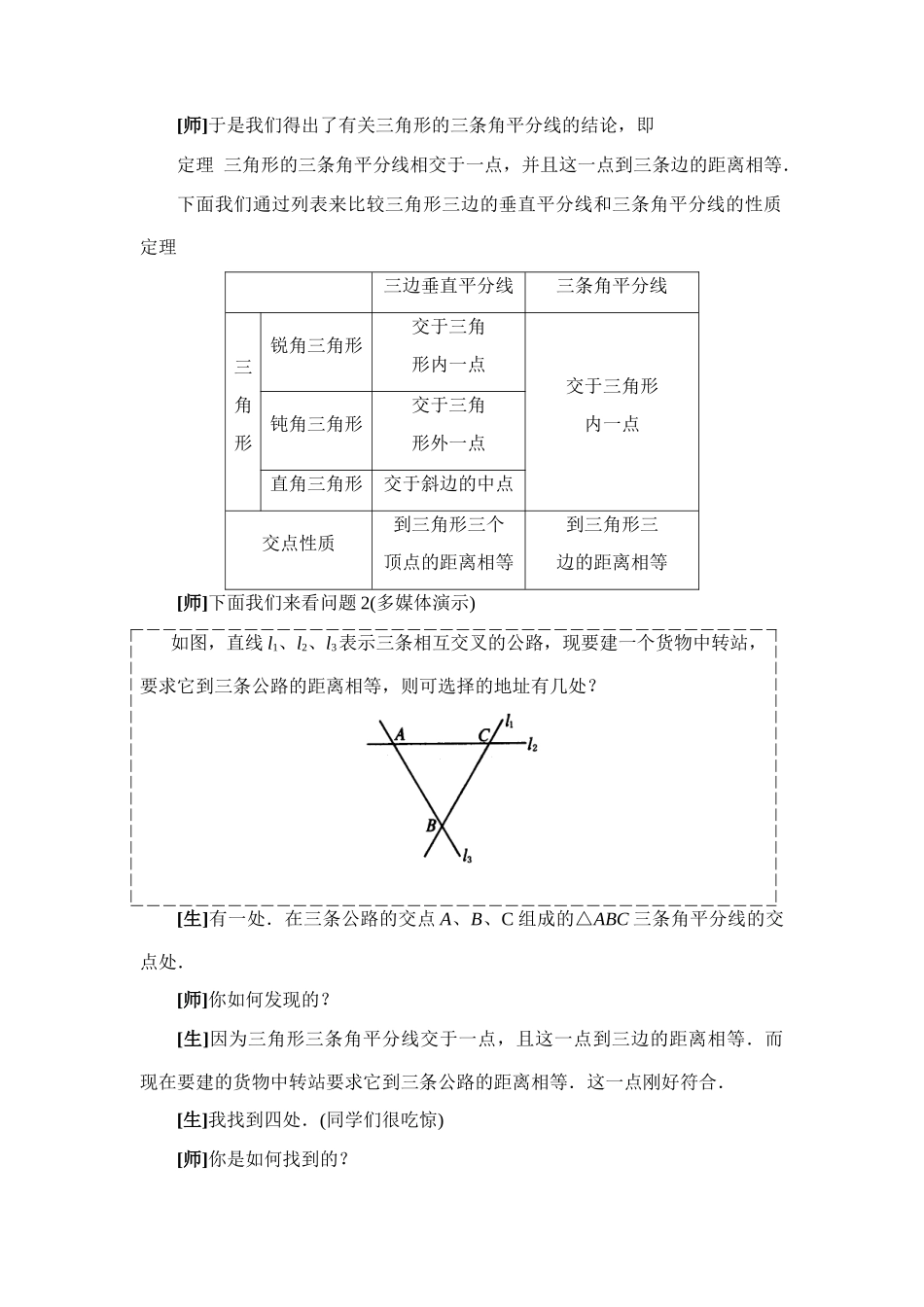
角平分线教学目标(一)教学知识点1.证明与角的平分线的性质定理和判定定理相关的结论.2.角平分线的性质定理和判定定理的灵活运用.(二)能力训练要求1.进一步发展学生的推理证明意识和能力.2.培养学生将文字语言转化为符号语言、图形语言的能力.3.提高综合运用数学知识和方法解决问题的能力.(三)情感与价值观要求1.能积极参与数学学习活动,对数学有好奇心和求知欲.2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.教学重点1.三角形三个内角的平分线的性质.2.综合运用角平分线的判定和性质定理,解决几何中的问题.教学难点角平分线的性质定理和判定定理的综合应用.教学方法活动探究法教具准备多媒体演示教学过程Ⅰ.设置情境问题,搭建探究平台问题1习题1.8的第1题作三角形的三个内角的角平分线,你发现了什么?(教师可用多媒体演示尺规作图过程).[生]三角形的三个内角的角平分线交于一点.[生]根据角平分线的性质定理还可知这点到三角形三边的距离相等.[师]你还可以用什么方法说明上述结论呢?[生]利用折纸.在纸板上画一个三角形并剪下来,折叠,作出三角形三个内角的角平分线交于一点.[师]如何利用我们学过的公理和已证的定理来证明它呢?可以类比我们学过的知识解决吗?[生]可以类比三角形三条边的垂直平分线交于一点的方法来证明.我们在证此结论时,先是设有其中两边的垂直平分线交于一点,然后利用线段垂直平分线的判定定理,说明这一点在第三边的垂直平分线上.[师]很好!下面我们就来证明:三角形三条角平分线相交于一点.Ⅱ.展示思维过程,构建探究平台[师生共析]已知:如图,设△ABC的角平分线BM、CN相交于点P,证明:P点在∠BAC的角平分线上.证明:过P点作PD⊥AB,PF⊥AC,PE⊥BC,其中D、E、F是垂足. BM是△ABC的角平分线,点P在BM上,∴PD=PE(角平分线上的点到这个角的两边的距离相等).同理:PE=PF.∴PD=PF.∴点P在∠BAC的平分线上(在一个角的内部,且到角两边距离相等的点,在这个角的平分线上).∴△ABC的三条角平分线相交于点P.[师]在证明过程中,我们除证明了三角形的三条角平分线相交于一点外,还证明了什么呢?[生]还证明了PD=PE=PF,即这个交点到三角形三边的距离相等.[师]于是我们得出了有关三角形的三条角平分线的结论,即定理三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.下面我们通过列表来比较三角形三边的垂直平分线和三条角平分线的性质定理三边垂直平分线三条角平分线三角形锐角三角形交于三角形内一点交于三角形内一点钝角三角形交于三角形外一点直角三角形交于斜边的中点交点性质到三角形三个顶点的距离相等到三角形三边的距离相等[师]下面我们来看问题2(多媒体演示)如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?[生]有一处.在三条公路的交点A、B、C组成的△ABC三条角平分线的交点处.[师]你如何发现的?[生]因为三角形三条角平分线交于一点,且这一点到三边的距离相等.而现在要建的货物中转站要求它到三条公路的距离相等.这一点刚好符合.[生]我找到四处.(同学们很吃惊)[师]你是如何找到的?[生]除了刚才同学找到的三角形ABC内部的一点外,我认为在三角形外部还有三点.作∠ACB、∠ABC外角的平分线交于点P1(如下图所示),我们利用角平分线的性质定理和判定定理,可知点P1在∠CAB的角平分线上,且到l1、l2、l3的距离相等.同理还有∠BAC、∠BCA的外角的角平分线的交点P2;∠BAC、∠CBA的外角的角平分线的交点P3.因此满足条件的点共4个,分别是P、P1、P2、P3.Ⅲ.例题讲解多媒体演示[例1]如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)已知CD=4cm,求AC的长;(2)求证:AB=AC+CD.分析:本例需要运用前面所学的多个定理,而且将计算和证明融合在一起,目的是使学生进一步理解、掌握这些知识和方法,并能综合运用它们解决问题第(1)问中,求AC的长,需求出BC的长,而BC=CD+DB,CD=4cm,而BD在等腰直角三角形DBE中,根据角平分线的性质,DE=CD=4cm,再...