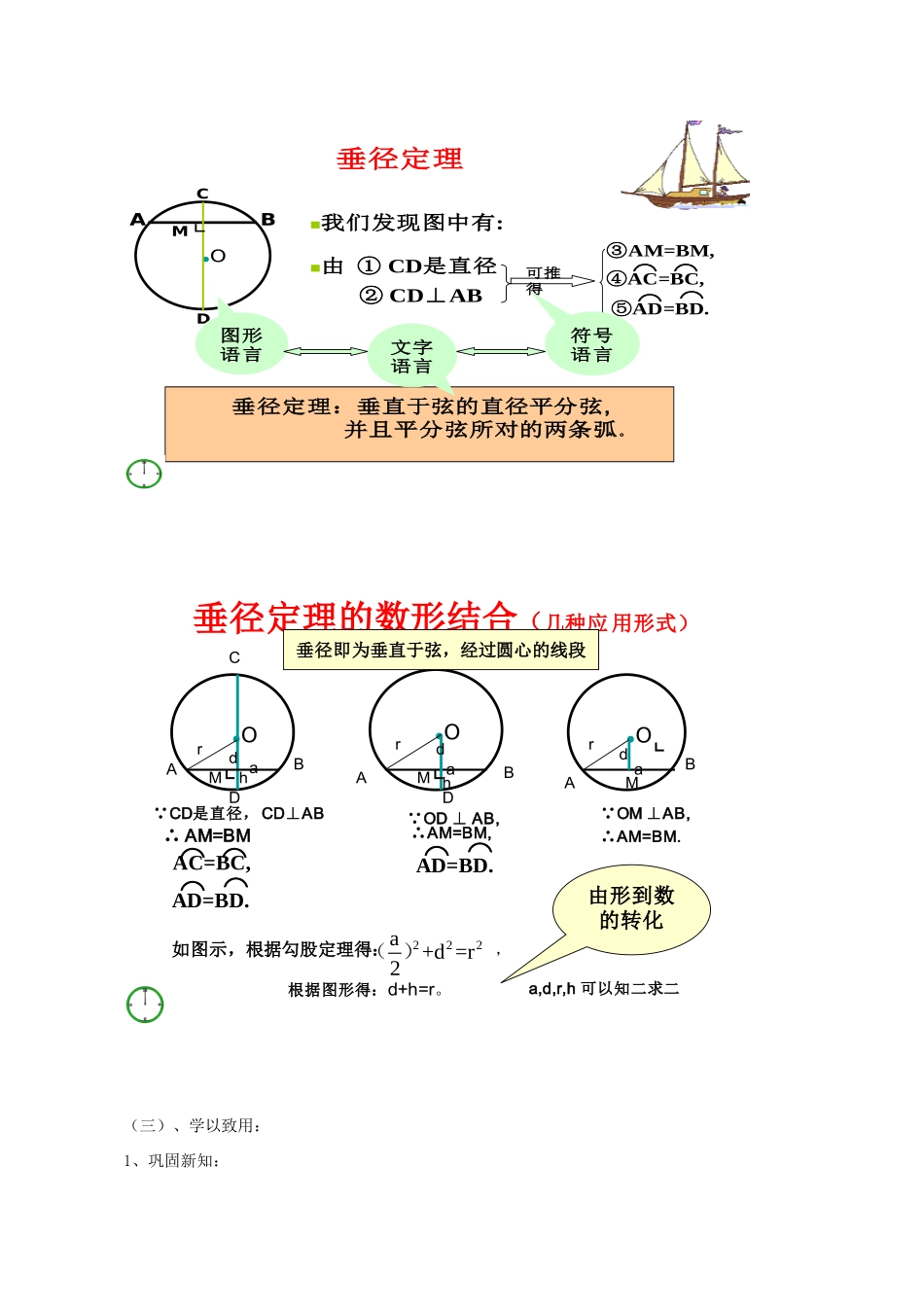
圆的对称性一、教与学目标:1.知道圆的轴对称性并能说出其对称轴.2.能说出垂径定理及其推论.3.能运用垂径定理及其推论进行有关的计算和证明.4.学习过程中,领悟转化思想和数形结合思想.二、教与学重点难点:能运用垂径定理及其推论进行有关的计算和证明。三、教与学方法:自主探究,合作交流四、教与学过程:(一)、情境导入:(1)你还记得什么是圆吗?你学过哪些有关圆的知识?(2)什么是轴对称图形?有什么特征?(3)我们采用什么方法研究轴对称图形?通过直接回忆相关知识引入新课,利于新知的学习。(二)、探究新知:1、问题导读:按下面的步骤做一做:在一张半透明的纸片上画一个圆,标出它的圆心O,并任意作出一条直径AB,将圆O沿直径AB折叠,你发现了什么?(自学课本68页交流与发现1,2)2、合作交流:(1)如图,CD是⊙O的直径,作弦AB,使CD⊥AB,记垂足为M.将⊙O沿直径CD折叠,你发现AC与AD有什么关系?BC与BD有什么关系?线段CE与DE有什么关系?(2)你能证明你的结论吗?(3)你能用语言表达你发现的结论吗?3、精讲点拨:③AM=BM,●O我们发现图中有:ABCDM└由①CD是直径②CD⊥AB可推得⌒⌒④AC=BC,⌒⌒⑤AD=BD.垂径定理垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。图形语言文字语言符号语言垂径定理的数形结合(几种应用形式)●O●O●O┗┗┗ABCDMABDMABM垂径即为垂直于弦,经过圆心的线段∴AM=BM⌒⌒AC=BC,⌒⌒AD=BD.∴AM=BM,⌒⌒AD=BD.∴AM=BM.∵OD⊥AB,∵OM⊥AB,radhradhrda如图示,根据勾股定理得:,根据图形得:d+h=r。222a+d=r2()∵CD是直径,CD⊥AB由形到数的转化a,d,r,h可以知二求二(三)、学以致用:1、巩固新知:EOABDCEABCDEOABDCOBAEEOABCEOCDAB练习在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧2、精讲例题例1、如图4,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD求证:OC=OD。例2、1300多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦长)为37.4m,拱高(弧的中点到弦的的距离,也叫弓形高)为7.2m。求桥拱的半径。(四)巩固提高1、两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系?为什么?2、如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.3、已知:AB和CD是⊙O内的两条平行弦,AB=6cm,CD=8cm,⊙O的半径为5cm,(1)请根据题意画出符合条件的图形;(2)求出AB、与CD间的距离。(五)课堂小结:(1)谈一谈,这节课你有哪些收获?(2)对于本节所学内容你还有哪些疑惑?(六)作业布置:习题4.11-2题五、教学反思垂径定理是中学数学中的一个很重要的定理,由于他涉及到的条件结论比较多,学生容易搞混肴,本节课采取了,讲练结合动手操作的教学方法,课前布置所有同学制作一张画好圆的纸片,课上利用此纸片探索、体验圆是轴对称图形,并进一步利用圆的轴对称性探究垂径定理,环环相扣、逐层深入,激发学生的学习兴趣,收到了很好的教学效果。教学中,学习水平不足的同学参与了活动完成的质量不够,费时较长,一定程度上影响了课堂进度,教师应加强适时点拔指导。