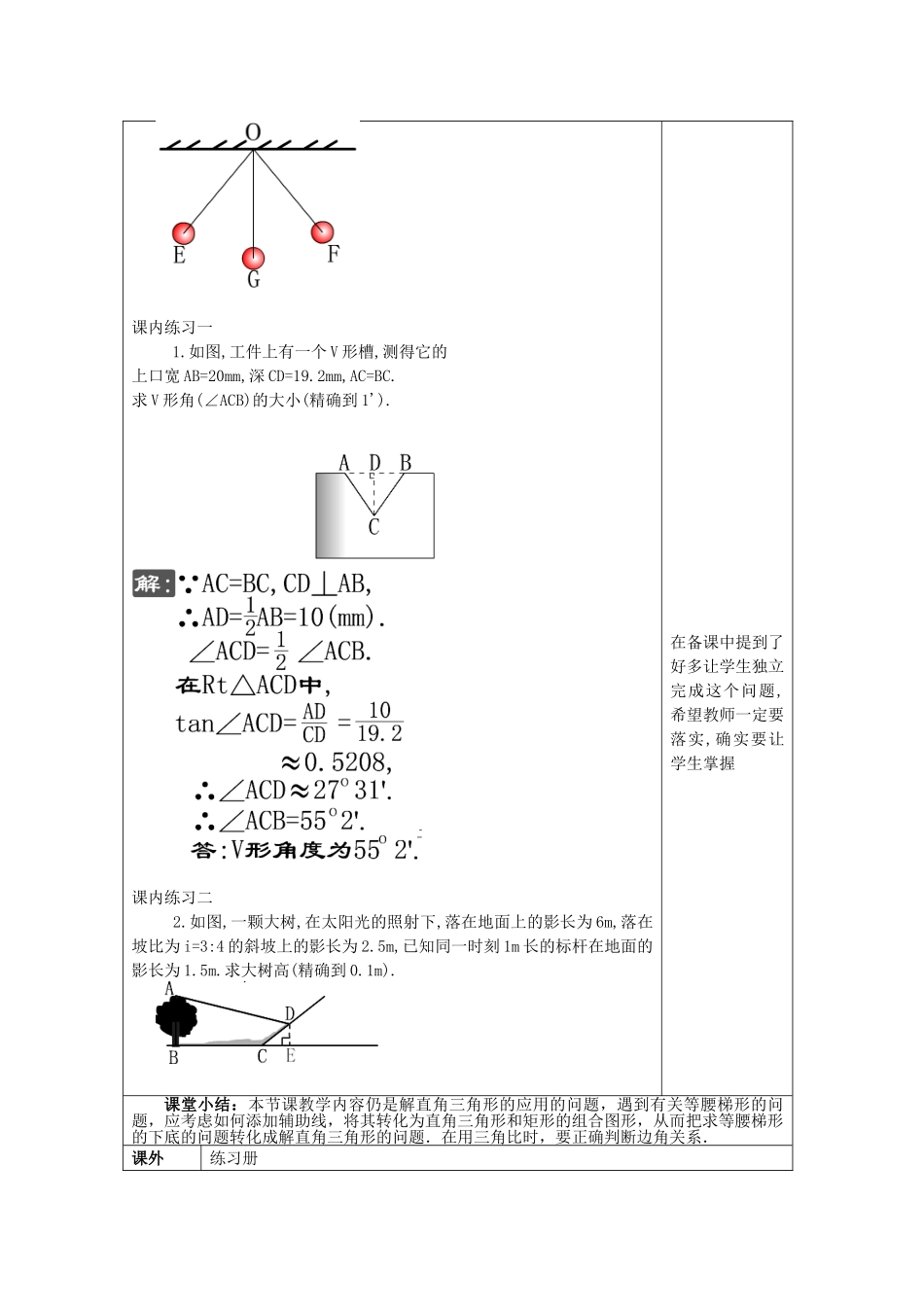
解直角三角形的应用课题25.4(5)解直角三角形的应用课型新授课教学目标1.理解什么是横断面图,能把一些较复杂的图形转化为解直角三角形的问题.2.逐步形成用数学的意识;渗透转化思想;渗透数学来源于实践又作用于实践的观点.重点把等腰梯形转化为解直角三角形问题难点如何添作适当的辅助线教学准备多媒体学生活动形式讲练结合教学过程设计意图课题引入:如图,在相距31.5米的两根等高电杆AB,CD间的点P处,测得电杆AB的顶点A的仰角为α,电杆CD的顶点C的仰角为β,且tanα=,sinβ=.求电杆的高(测角仪高度忽略不计).知识呈现:新课探索一例题1如图所示的工件叫做燕尾槽,它的横断面是一个等腰三角形,∠B叫做燕尾角,AD叫做外口,BC叫做里口,AE叫做燕尾槽深度.已知AD长180毫米,BC长300毫米,AE长70毫米,那么燕尾角B的大小是多少(精确到1')?新课探索二例题2如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在左,右两个最高位置时,细绳相应所成的角为40.求小球在最高位置和最低位置时的高度差(精确到0.1厘米).课内练习一1.如图,工件上有一个V形槽,测得它的上口宽AB=20mm,深CD=19.2mm,AC=BC.求V形角(∠ACB)的大小(精确到1').课内练习二2.如图,一颗大树,在太阳光的照射下,落在地面上的影长为6m,落在坡比为i=3:4的斜坡上的影长为2.5m,已知同一时刻1m长的标杆在地面的影长为1.5m.求大树高(精确到0.1m).在备课中提到了好多让学生独立完成这个问题,希望教师一定要落实,确实要让学生掌握课堂小结:本节课教学内容仍是解直角三角形的应用的问题,遇到有关等腰梯形的问题,应考虑如何添加辅助线,将其转化为直角三角形和矩形的组合图形,从而把求等腰梯形的下底的问题转化成解直角三角形的问题.在用三角比时,要正确判断边角关系.课外练习册作业预习要求教学后记与反思1、课堂时间消耗:教师活动分钟;学生活动分钟)2、本课时实际教学效果自评(满分10分):分3、本课成功与不足及其改进措施: