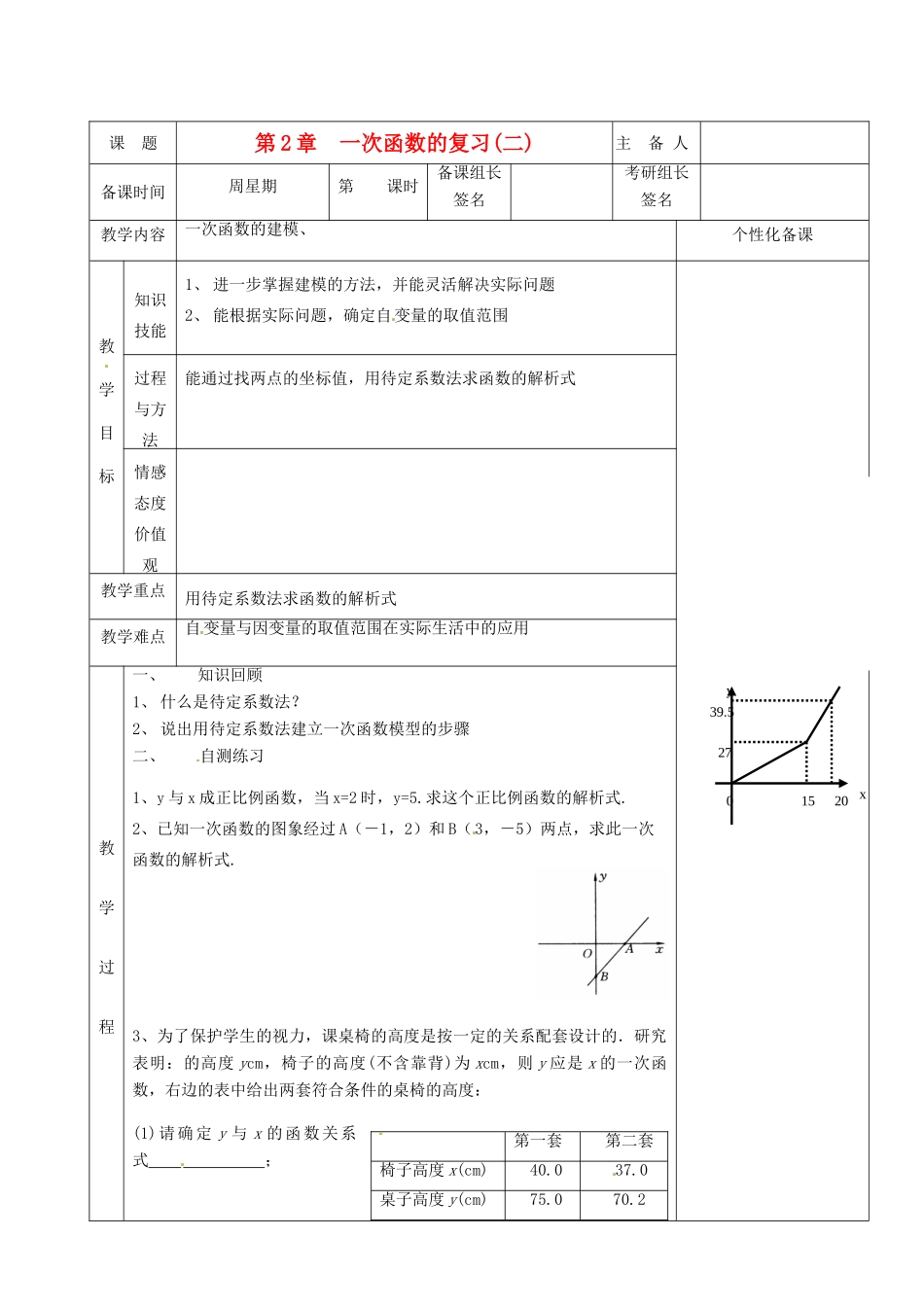
0yx15202739.5课题第2章一次函数的复习(二)主备人备课时间周星期第课时备课组长签名考研组长签名教学内容一次函数的建模、个性化备课教学目标知识技能1、进一步掌握建模的方法,并能灵活解决实际问题2、能根据实际问题,确定自变量的取值范围过程与方法能通过找两点的坐标值,用待定系数法求函数的解析式情感态度价值观教学重点用待定系数法求函数的解析式教学难点自变量与因变量的取值范围在实际生活中的应用教学过程一、知识回顾1、什么是待定系数法?2、说出用待定系数法建立一次函数模型的步骤二、自测练习1、y与x成正比例函数,当x=2时,y=5.求这个正比例函数的解析式.2、已知一次函数的图象经过A(-1,2)和B(3,-5)两点,求此一次函数的解析式.3、为了保护学生的视力,课桌椅的高度是按一定的关系配套设计的.研究表明:的高度ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数,右边的表中给出两套符合条件的桌椅的高度:(1)请确定y与x的函数关系式;第一套第二套椅子高度x(cm)40.037.0桌子高度y(cm)75.070.20yx15202739.5(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌,它们是否配套?请通过计算说明理由4、某自来水公司为鼓励居民节约用水,采取按月用水量收费办法,若某户居民应交水费x元)与用水量x吨)的函数关系如图所示。(1)分别写出当0≤x≤15和x>15时,y与x函数关系式;(2)若某户该月用水21吨,则应交水费多少元?三、达标练习、1、某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:若日销售量y是销售价x的一次函数.(1)求出日销售量y(件)与销售价x(元)的函数关系式:(2)如果某天销售了15件,此日销售利润是多少元?2、图9是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:(1)汽车在前9分钟内的平均速度是(2)汽车在中途停了多长时间?(3)当16≤t≤30时,求S与t的函数关系式.3、(2011四川南充市,20,8分)某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数图象如图:(1)、写出y与x的函数关系式(2)、当电价为600元千度时,工厂消耗每千度电产生利润是多少?(3)、当每千度电价为多少元时,工厂就要亏本?教学反x(元/千度)y(元/千度)500300200O091630t/minS/km4012x(元)152030…y(件)252010…思