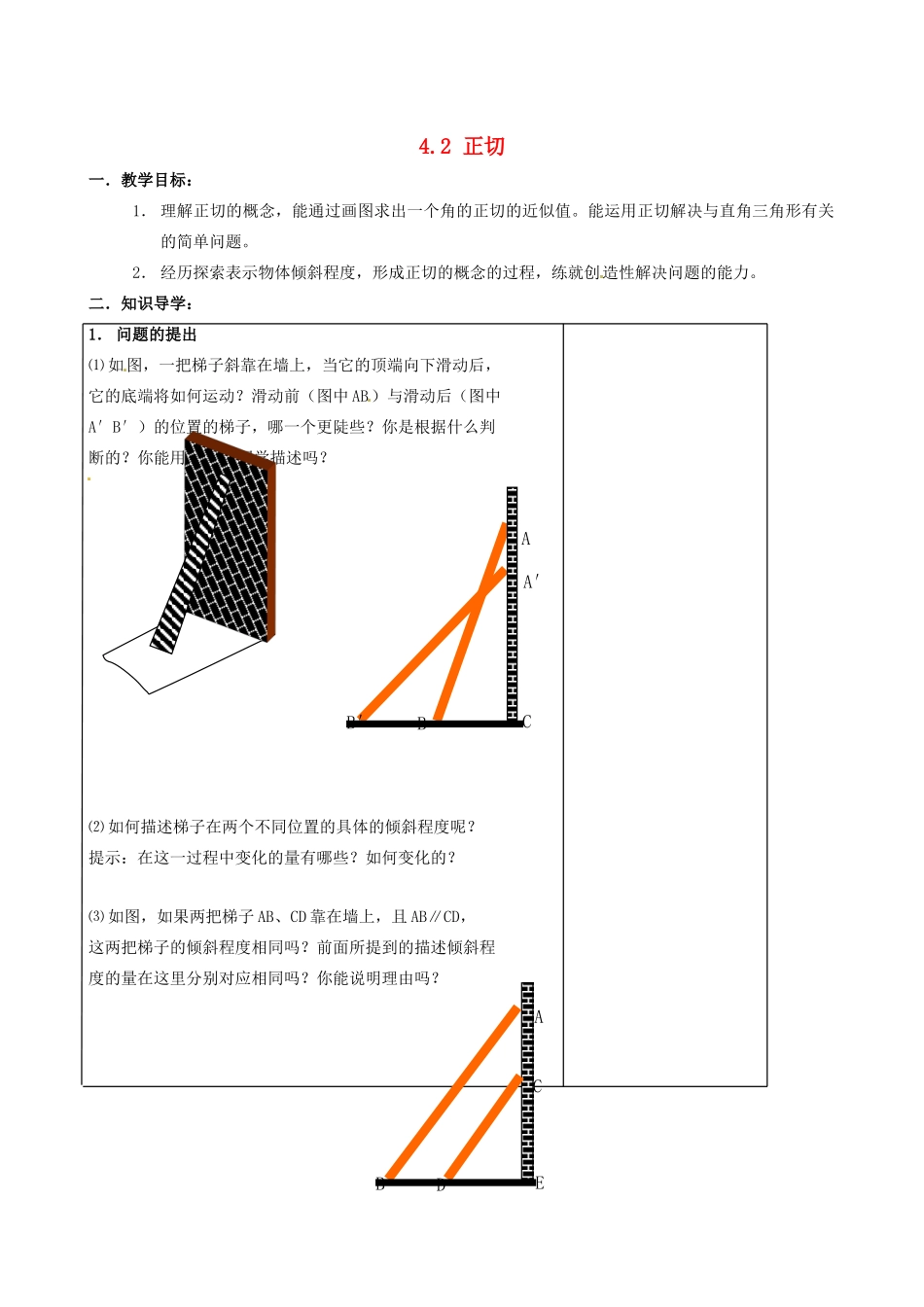
4.2正切一.教学目标:1.理解正切的概念,能通过画图求出一个角的正切的近似值。能运用正切解决与直角三角形有关的简单问题。2.经历探索表示物体倾斜程度,形成正切的概念的过程,练就创造性解决问题的能力。二.知识导学:1.问题的提出⑴如图,一把梯子斜靠在墙上,当它的顶端向下滑动后,它的底端将如何运动?滑动前(图中AB)与滑动后(图中A′B′)的位置的梯子,哪一个更陡些?你是根据什么判断的?你能用语言向同学描述吗?⑵如何描述梯子在两个不同位置的具体的倾斜程度呢?提示:在这一过程中变化的量有哪些?如何变化的?⑶如图,如果两把梯子AB、CD靠在墙上,且AB∥CD,这两把梯子的倾斜程度相同吗?前面所提到的描述倾斜程度的量在这里分别对应相同吗?你能说明理由吗?BAA′B′CDACBE2.问题的发展一般地,如果锐角A的大小确定,我们可以作出无数个以A为一个锐角直角三形(如图),那么图中:成立吗?为什么?⑴当∠A变化时,上面等式仍然成立吗?⑵上面等式的值随∠A的变化而变化吗?3.概念的形成由前面的探索可以看出:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。这个比值反映了斜边相对于这角的邻边的倾斜程度,它与这个锐角的大小有着密切的关系。在直角三角形中,我们将∠A的对边与它的邻边的比称为∠A的正切,记作tanA即:4.一个锐角的正切值⑴如图,△ABC中,AC=4,BC=3,∠C=90°,求:tanA与tanB的值。⑵你能用画图的方法计算一个50°角的正切的近似值吗?ABB1B2CC1C2ABCabABC34⑶如图,从点O出发,点P沿65°线移动,当在水平方向上向右前进了一个单位时,它在垂直方向上向上前进了个单位。P点的坐标是,tan65°≈。据图填表:①想一想:锐角的正切值是如何随着的变化而变化的?0°20°30°45°55°65°75°43.532.521.510.51858075706560555045403530252015105②关于用计算器计算正切值请课后自学。三.巩固与拓展1.基础巩固⑴某楼梯的踏板宽为30cm,一个台阶的高度为15cm,求楼梯倾斜角的正切值。⑵如图,在Rt△ABC中,∠C=90°,AB=5,BC=,求tanA与tanB的值。⑶如图,在Rt△ABC中,∠C=90°,BC=12,tanA=求AB的值。2.拓展延伸⑴如图,在在Rt△ABC中,∠ACB=90°,CD是AB边上的高,①tanA==;②tanB==;③tan∠ACD=;④tan∠BCD=;⑵如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,求树的高度是多少?⑶如图4,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,求路灯A的高AB。附.作业:课本P51T1-①、T2四.收获与体会ABCBACABCDABCDEF