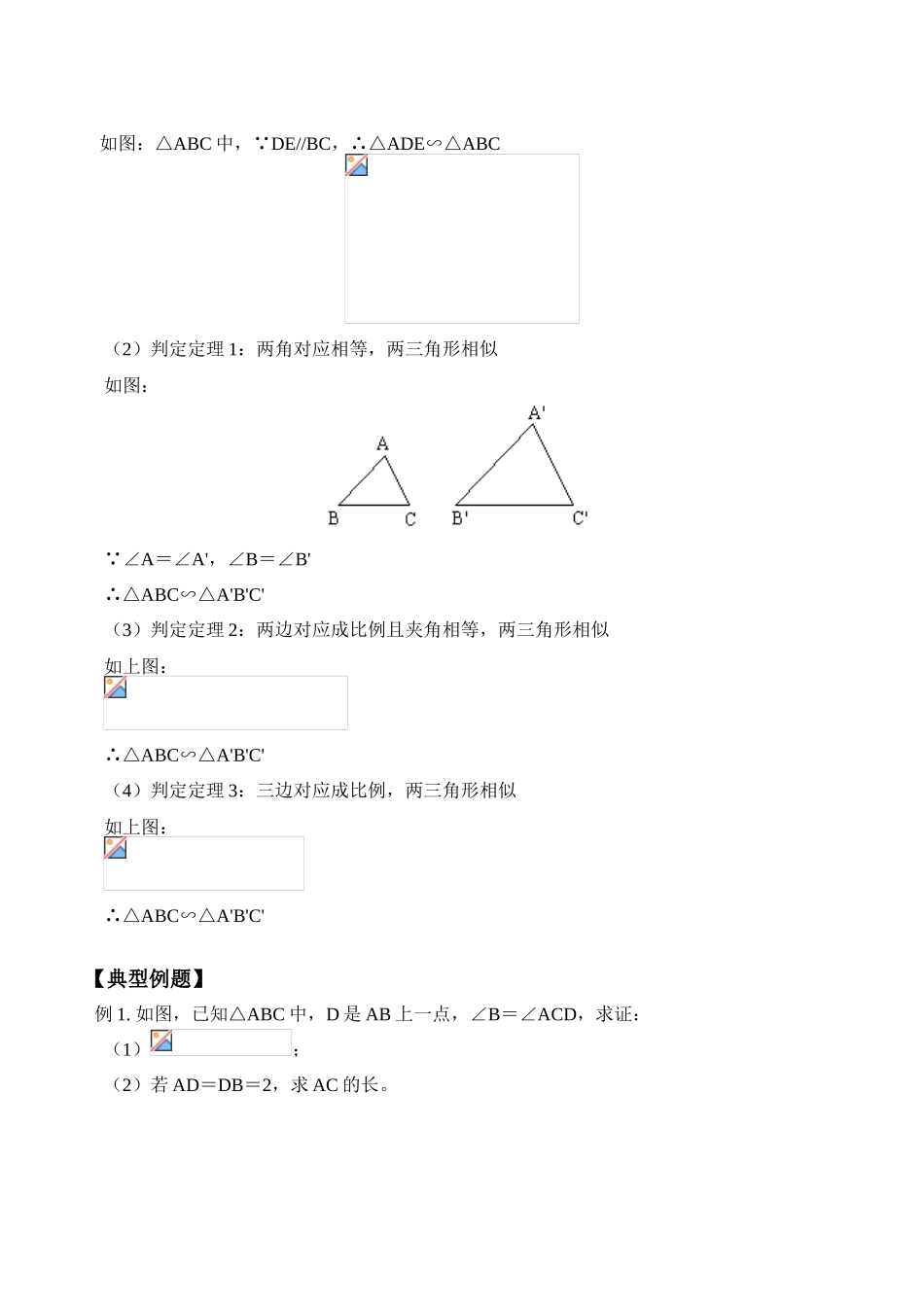
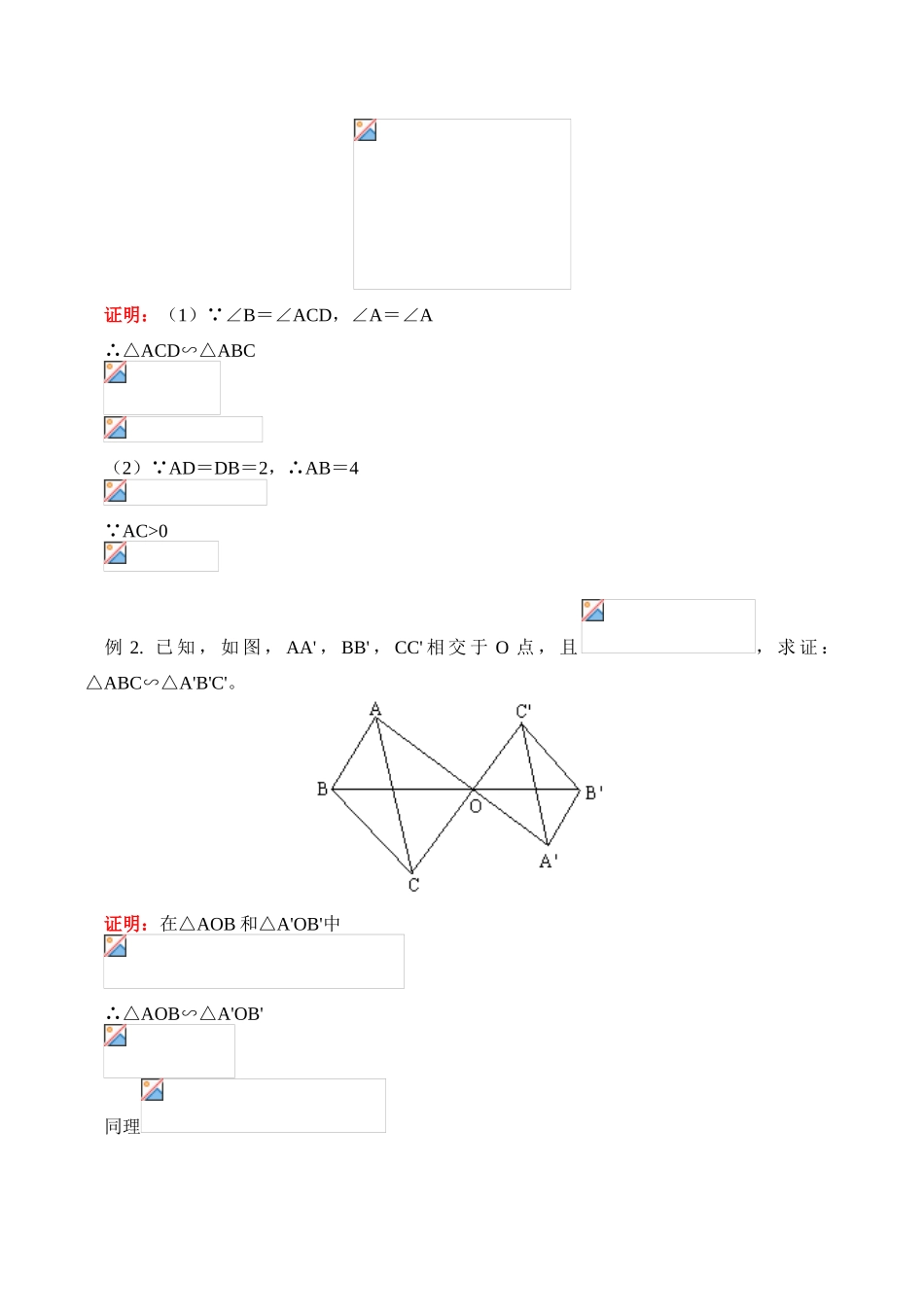
一.教学内容:第十九章:相似形19.4相似多边形19.5相似三角形的判定教学目标:1.了解相似多边形的概念、性质。2.理解相似三角形的概念,探索并掌握相似三角形的判定、性质。3.能利用相似三角形的基本性质解决一些简单的问题。二.重点、难点:重点:相似三角形的判定。难点:相似三角形成比例线段的选取。教学过程:(一)知识要点:1.相似多边形对应角相等,对应边成比例的两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比(相似系数)。“相似于”用“∽”表示。由相似多边形定义可知:相似多边形对应角相等,对应边成比例。2.相似三角形相似三角形是最简单的相似多边形。三个角对应相等,三边对应成比例的三角形是相似三角形。如:△ABC∽△A'B'C'由定义可知:注:相似多边形,相似三角形对应元素应写在对应的位置上。3.相似三角形的判定(1)预备定理:平行于三角形一边的直线,截其他两边所得的三角形和原三角形相似。如图:△ABC中,∵DE//BC,∴△ADE∽△ABC(2)判定定理1:两角对应相等,两三角形相似如图:∵∠A=∠A',∠B=∠B'∴△ABC∽△A'B'C'(3)判定定理2:两边对应成比例且夹角相等,两三角形相似如上图:∴△ABC∽△A'B'C'(4)判定定理3:三边对应成比例,两三角形相似如上图:∴△ABC∽△A'B'C'【典型例题】例1.如图,已知△ABC中,D是AB上一点,∠B=∠ACD,求证:(1);(2)若AD=DB=2,求AC的长。证明:(1)∵∠B=∠ACD,∠A=∠A∴△ACD∽△ABC(2)∵AD=DB=2,∴AB=4∵AC>0例2.已知,如图,AA',BB',CC'相交于O点,且,求证:△ABC∽△A'B'C'。证明:在△AOB和△A'OB'中∴△AOB∽△A'OB'同理又∴△ABC∽△A'B'C'例3.已知,如图△ABC中,D是BC上一点,EG//BC,分别交AB、AD、AC于E,F、G,求证:EF·DC=FG·BD分析:将等积式改写成比例式,得,设法利用相似三角形解得,,从而使问题得到解决。证明:在△AEF和△ABD中∵EF//BD∴△AEF∽△ABD同理∴EF·DC=FG·BD例4.已知,如图△ABC中,AB=AC,延长AB到D,使BD=AB,E是AB中点,求证:分析:由于图中相等线段及线段中点较多,可设法利用三角形相似加以解决。证明:∵AB=AC=BD,AE=EB又∵∠EAC=∠DAC∴△AEC∽△ACD即例5.已知,如图平行四边形ABCD中,E是CB延长线上一点,DE交AB于F,求证:BC·CD=AF·CE分析:由于△ADF∽△CED,可得,再通过AD=BC,由等量代换即可得证。证明:∵四边形ABCD是平行四边形∴AD=BC,∠A=∠C,AD//CE∴∠ADF=∠E∴△ADF∽△CED∴BC·CD=AF·CE例6.已知,如图AB、CD交于O点,AC//BD,E是AC中点,EO的延长线交BD于F点,求证:F是BD中点。分析:利用图中AE=CE,设法找到DF、BF与AE、CE的联系,即证出证明:∵AC//BD∴△AOE∽△BOF同理∵AE=CE∴BF=DF即F是BD中点三.小结:在相似三角形成比例线段中,较线段相等线段多了。同学们要特别注意,另外同学们要注意方法的总结,证明相似三角形的方法,线段相等的方法,角相等的方法、比例式、等积式等比代换(如何选取中间比)【模拟试题】(答题时间:30分钟)1.已知,如图平行四边形ABCD中,E是AB延长线上一点,DE交BC于F,求证:BC·CD=CF·AE。2.已知,如图△ABC中,D是BC中点,E是AD上一点,CE的延长线交AB于F,求证:AE:ED=2AF:FB。3.已知,如图△ABC中,D是BC上一点,EG//BC,分别交AB、AD、AC于E、F、G。求证:EF·DC=FG·BD。4.已知,如图△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AD于E,交BC延长线于F,求证:。5.已知,如图梯形ABCD中,AB//CD,AE//BC交BD的延长线于E,AC交BD于F,求证:FB2=FD·FE。试题答案1.提示:证△ADE∽△CFD,得有AD·CD=AE·CF,由AD=BC可得结论。2.提示:过D作DM//CF交AB于M点。3.提示:证△AEF∽△ABD,△AFG∽△ADC,可得,可得结论。4.提示:连结AF,证△ABF∽△ACF。5.提示:证△DFC∽△AFB,△AEF∽△CBF。