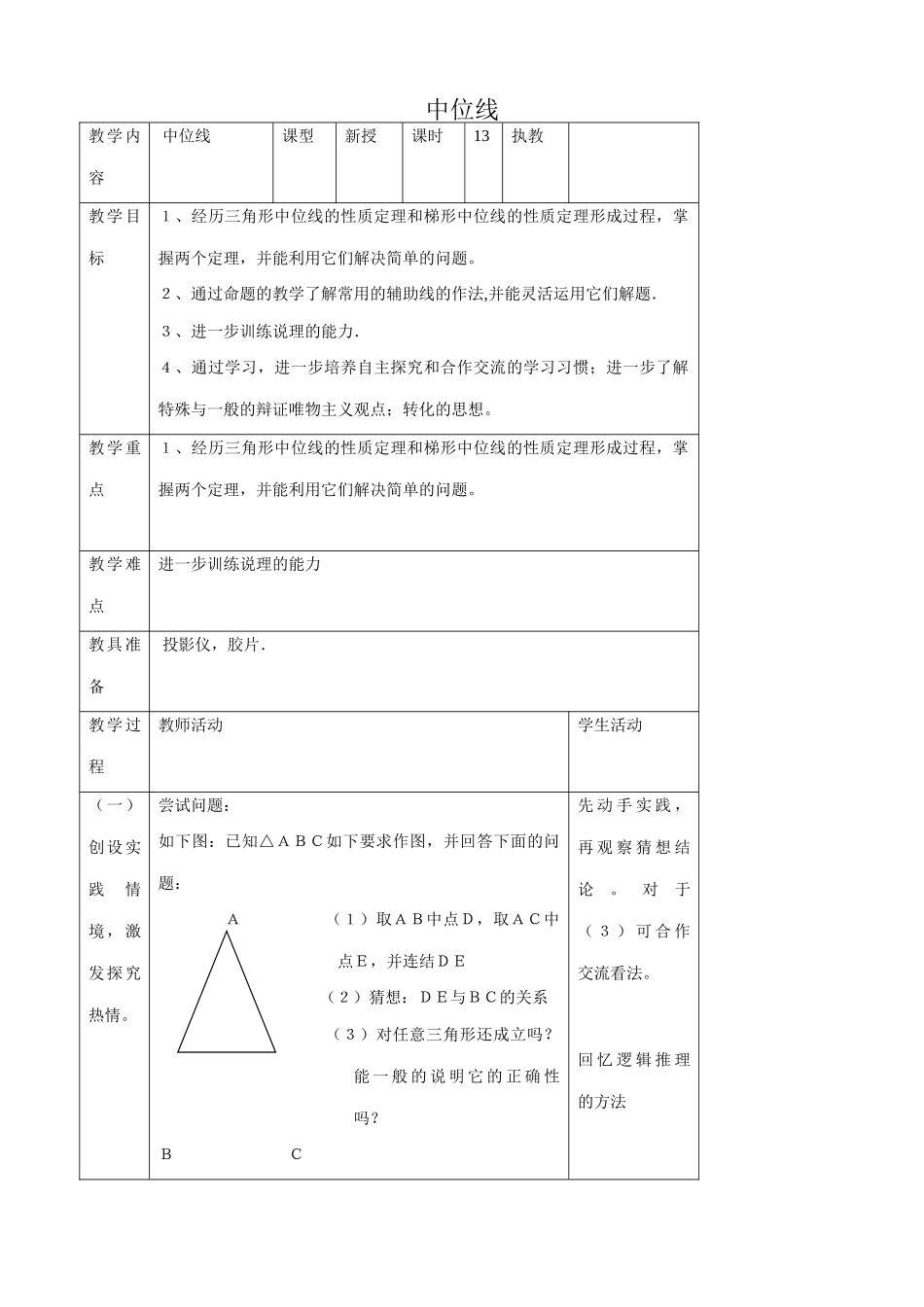
中位线教学内容中位线课型新授课时13执教教学目标1、经历三角形中位线的性质定理和梯形中位线的性质定理形成过程,掌握两个定理,并能利用它们解决简单的问题。2、通过命题的教学了解常用的辅助线的作法,并能灵活运用它们解题.3、进一步训练说理的能力.4、通过学习,进一步培养自主探究和合作交流的学习习惯;进一步了解特殊与一般的辩证唯物主义观点;转化的思想。教学重点1、经历三角形中位线的性质定理和梯形中位线的性质定理形成过程,掌握两个定理,并能利用它们解决简单的问题。教学难点进一步训练说理的能力教具准备投影仪,胶片.教学过程教师活动学生活动(一)创设实践情境,激发探究热情。尝试问题:如下图:已知△ABC如下要求作图,并回答下面的问题:A(1)取AB中点D,取AC中点E,并连结DE(2)猜想:DE与BC的关系(3)对任意三角形还成立吗?能一般的说明它的正确性吗?BC先动手实践,再观察猜想结论。对于(3)可合作交流看法。回忆逻辑推理的方法(二)自主探究与合作交流研究三角形的中位线性质定理与梯形中位线性质定理。首先介绍三角形的中位线,梯形中位线的概念,并强调指出它与三角形中线的区别。(一)三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。老师指导学生写出已知、求证并引导学生分析证明方法:已知:如图27.3.11所示,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,DE=BC.分析:要证DE∥BC,DE=BC,可延长DE到F,使EF=DE,于是本题就转化为证明DF=BC,DE∥BC,故只要证明四边形BCFD为平行四边形.学生在老师的指导下写出已知和求证,并合作交流证明方法。思考:本题还有其它的解法吗?可引导作如下的辅助线作法。(二)梯形的中位线定理:梯形中位线定理梯形的中位线平行于两底边,并且等于两底和的一半.已知:如图27.3.12所示,在梯形ABCD中,AD∥BC,AE=BE,DF=CF.求证:EF∥BC,EF=(AD+BC).分析由于本题结论与三角形中位线定理的结论比较接近,可以连结AF,并延长AF交BC的延长线于G,证明的关键在于说明EF为△ABG的中位线.于是本题就转化为证明AF=GF,AD=CG,故只要证明△ADF≌△GCF.与自己的想法对照,一题多解,培养自己的发散思维能力。仿照上一定理的证明过程,独立完成。并归纳常用的辅助线作法。(三)应用与拓展例3求证三角形的一条中位线与第三边上的中线互相平分.已知:如图27.3.13所示,在△ABC中,AD=DB,BE=EC,AF=FC.求证:AE、DF互相平分.证明连结DE、EF.因为AD=DB,BE=EC,所以DE∥AC(三角形中位线定理)同理EF∥AB.所以四边形ADEF是平行四边形(平行四边形的定义).因此AE、DF互相平分(平行四边形的对角线互相平分).自主探究证法,指派一名学生谈思路。合作交流,共同研究常用辅助线作法。[同步训练]如图,在△ABC中,AB=AC,D、E、F分别是AB、BC、CA的中点.求证:四边形ADEF是菱形.独立思考后请一生谈思路。(四)小结与作业小结:谈一下你有哪些收获?作业:P61第8题各抒己见。(五)板书设计课题:中位线例题:名称图形定理三角形的中位线梯形的中位线(六)教后记