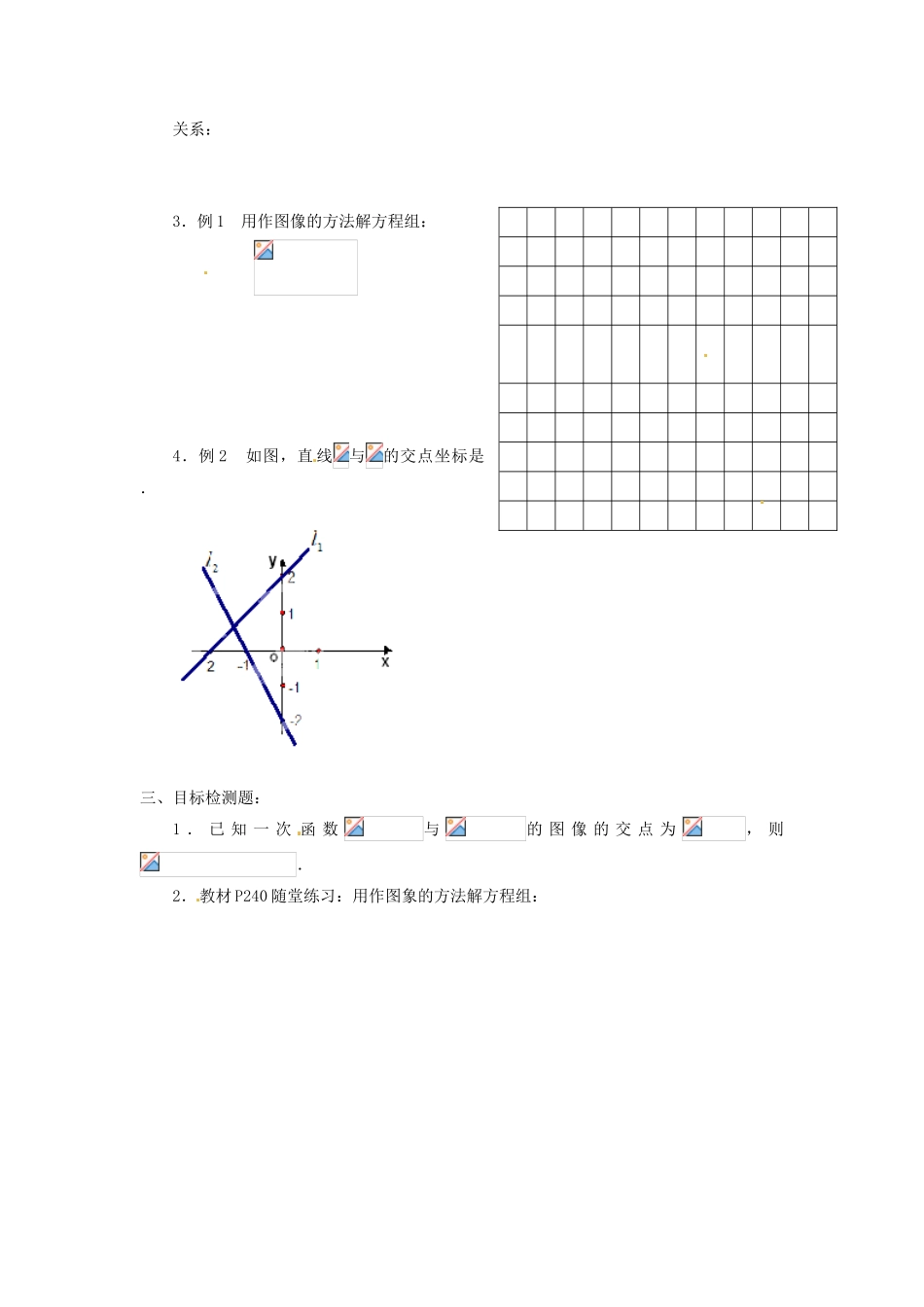
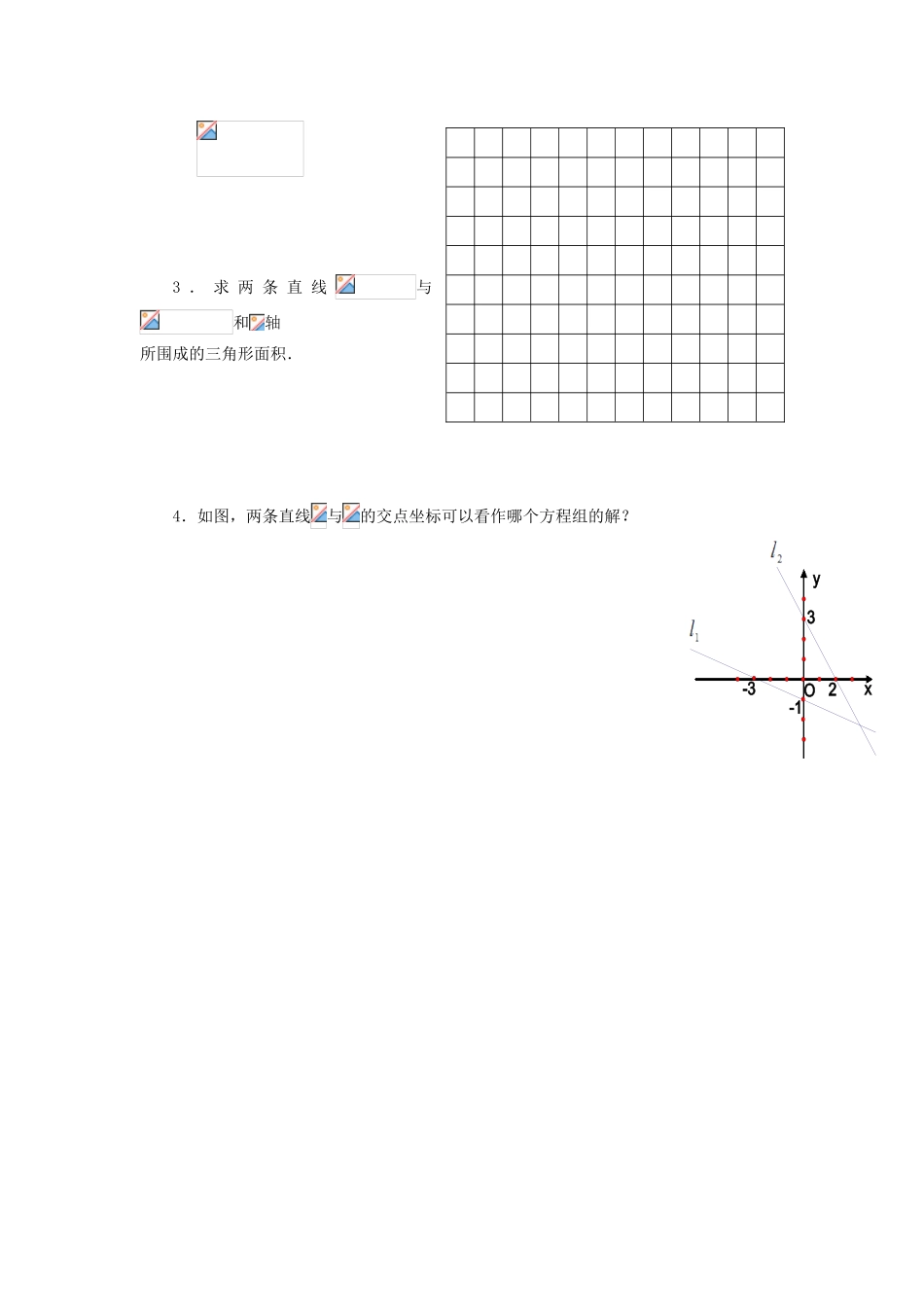
《7.6二元一次方程与一次函数(一)》一、学习目标:(1)初步理解二元一次方程和一次函数的关系;(2)掌握二元一次方程组和对应的两条直线之间的关系;(3)掌握二元一次方程组的图像解法.二、问题与题例:1.问题1:(课前思考)(1)方程x+y=5的解有多少个?是这个方程的解吗?(2)点(0,5),(5,0),(2,3)在一次函数y=的图像上吗?(3)在一次函数y=的图像上任取一点,它的坐标适合方程x+y=5吗?(4)以方程x+y=5的解为坐标的所有点组成的图像与一次函数y=的图像相同吗?2.问题2:(1)解方程组(2)上述方程移项变形转化为两个一次函数y=和y=2x,在同一直角坐标系内分别作出这两个函数的图像.(3)方程组的解和这两个函数的图像的交点坐标有什么关系?关系:3.例1用作图像的方法解方程组:4.例2如图,直线与的交点坐标是.三、目标检测题:1.已知一次函数与的图像的交点为,则.2.教材P240随堂练习:用作图象的方法解方程组:2O3-1-3yx3.求两条直线与和轴所围成的三角形面积.4.如图,两条直线与的交点坐标可以看作哪个方程组的解?四、配餐作业题:A组巩固基础1.教材P240《知识技能》1、2题.(1)用作图象的方法解方程组:(2)一次函数与的图象的交点为P(1,-2),试确定方程组的解和b的值。2.以方程2x+y=5的解为坐标的所有点组成的图象与一次函数____________的图象相同.3.一次函数y=7-4x和y=1-x的图象的交点坐标为_______,则方程组的解为_______________.B组强化训练1.已知函数的图象交于点P,则点P的坐标为().A.(-7,-3)B.(3,-7)C.(-3,-7)D.(-3,7)2.已知直线与直线相交于点,则b,m的值分别为().A.2,3B.3,2C.D.3.如果是方程组的解,则一次函数y=mx+n的解析式为()A.y=-x+2B.y=x-2C.y=-x-2D.y=x+24.一次函数的图象过点A(5,3)且平行于直线y=3x-,则这个函数的解析式为__________________。5.无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在第__________象限.6.已知两直线y1=2x-3,y2=6-x.(1)在同一坐标系中作出它们的图象.(2)求它们的交点A的坐标.(3)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.(4)求这两条直线与x轴所围成的△ABC的面积.C组延伸拓广1.已知y1=-x-4,y2=2ax+4a+b.(1)求a、b为何值时,两函数的图象重合?(2)如果两直线相交于点(-1,3),求a、b的值.