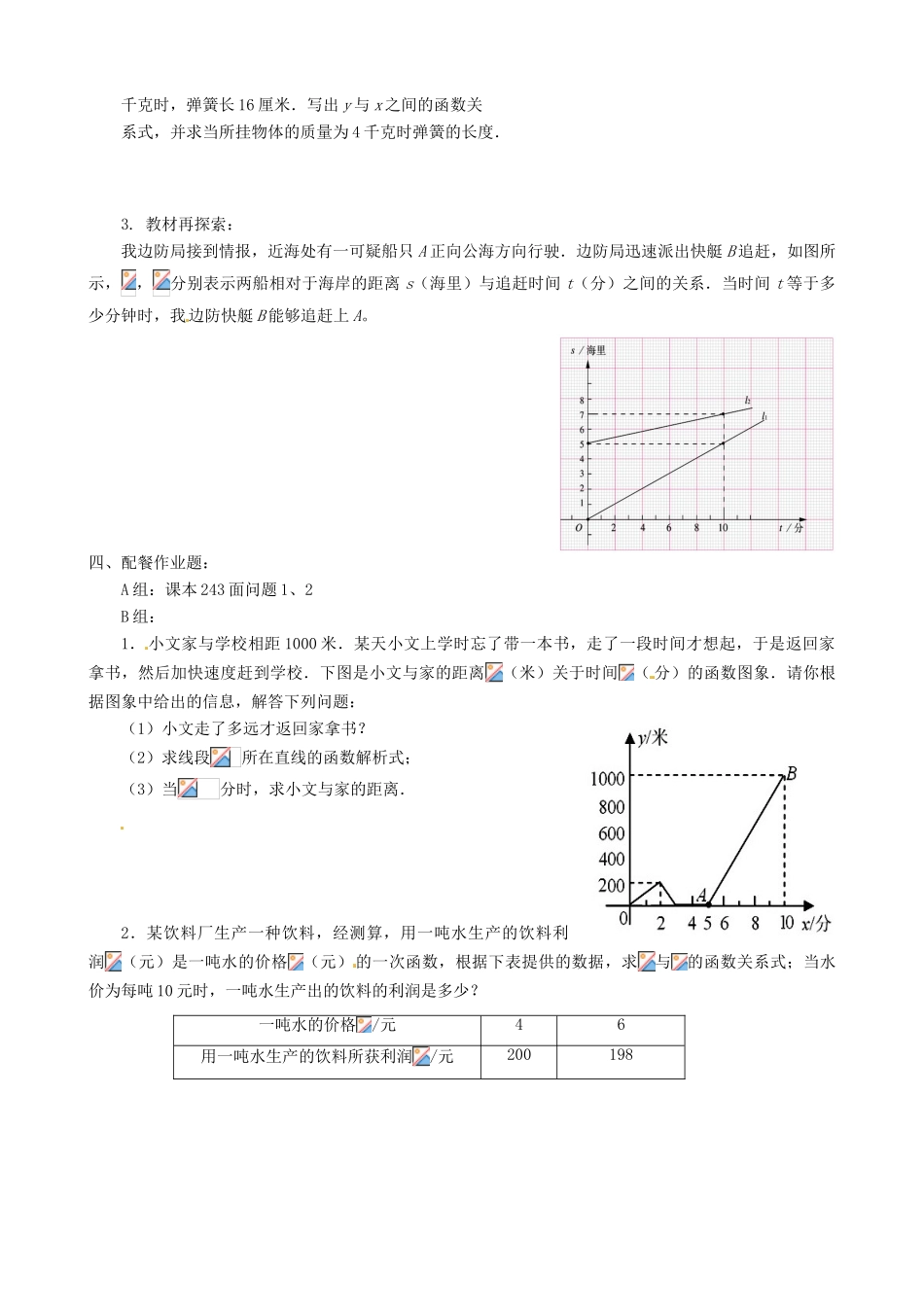
《7.6二元一次方程与一次函数(二)》一、学习目标:1.理解作函数图像的方法与代数方法各自的特点.2.掌握利用二元一次方程组确定一次函数的表达式.3.进一步理解方程与函数的联系.二、问题与题例:问题1:内容:教材议一议A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.1小时后乙距离A地80千米;2小时后甲距离A地30千米.问经过多长时间两人将相遇?例1某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数.现知李明带了60千克的行李,交了行李费5元,张华带了90千克的行李,交了行李费10元.(1)写出y与x之间的函数表达式;(2)旅客最多可免费携带多少千克的行李?例2某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;(2)若某用户十月份用水量为10吨,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?三、目标检测题:1.图中的两条直线,的交点坐标可以看做方程组的解2.在弹性限度内,弹簧的长度y(厘米)是所挂物体质量x(千克)的一次函数.当所挂物体的质量为1千克时弹簧长15厘米;当所挂物体的质量为3oyx12341234千克时,弹簧长16厘米.写出y与x之间的函数关系式,并求当所挂物体的质量为4千克时弹簧的长度.3.教材再探索:我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶,如图所示,,分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.当时间t等于多少分钟时,我边防快艇B能够追赶上A。四、配餐作业题:A组:课本243面问题1、2B组:1.小文家与学校相距1000米.某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校.下图是小文与家的距离(米)关于时间(分)的函数图象.请你根据图象中给出的信息,解答下列问题:(1)小文走了多远才返回家拿书?(2)求线段所在直线的函数解析式;(3)当分时,求小文与家的距离.2.某饮料厂生产一种饮料,经测算,用一吨水生产的饮料利润(元)是一吨水的价格(元)的一次函数,根据下表提供的数据,求与的函数关系式;当水价为每吨10元时,一吨水生产出的饮料的利润是多少?一吨水的价格/元46用一吨水生产的饮料所获利润/元200198C组:1.我们学校准备添置一批电脑,有两个方案可供选择:方案1:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装工工资等其他费用合计3000元.设学校需要电脑x台,方案1与方案2的费用分别为y1,y2元.(1)分别写出y1,y2的函数解析式;(2)当学校添置多少台电脑时,两种方案的费用相同?(3)若我们学校需要添置台电脑50台,你认为采用哪一种方案较省钱?说说你的理由2.如图,把矩形纸片OABC放入直角坐标系中,使OA,OC分别落在轴、轴的正半轴上,连接AC,将翻折,点B落在该坐标平面内,设这个落点为D,CD交轴于点E,已知CB=8,AB=4.(1)求AC所在直线的函数关系式;(2)求点E的坐标和的面积;(3)求点D的坐标,并判断点(8,)是否在直线OD上,说明理由.