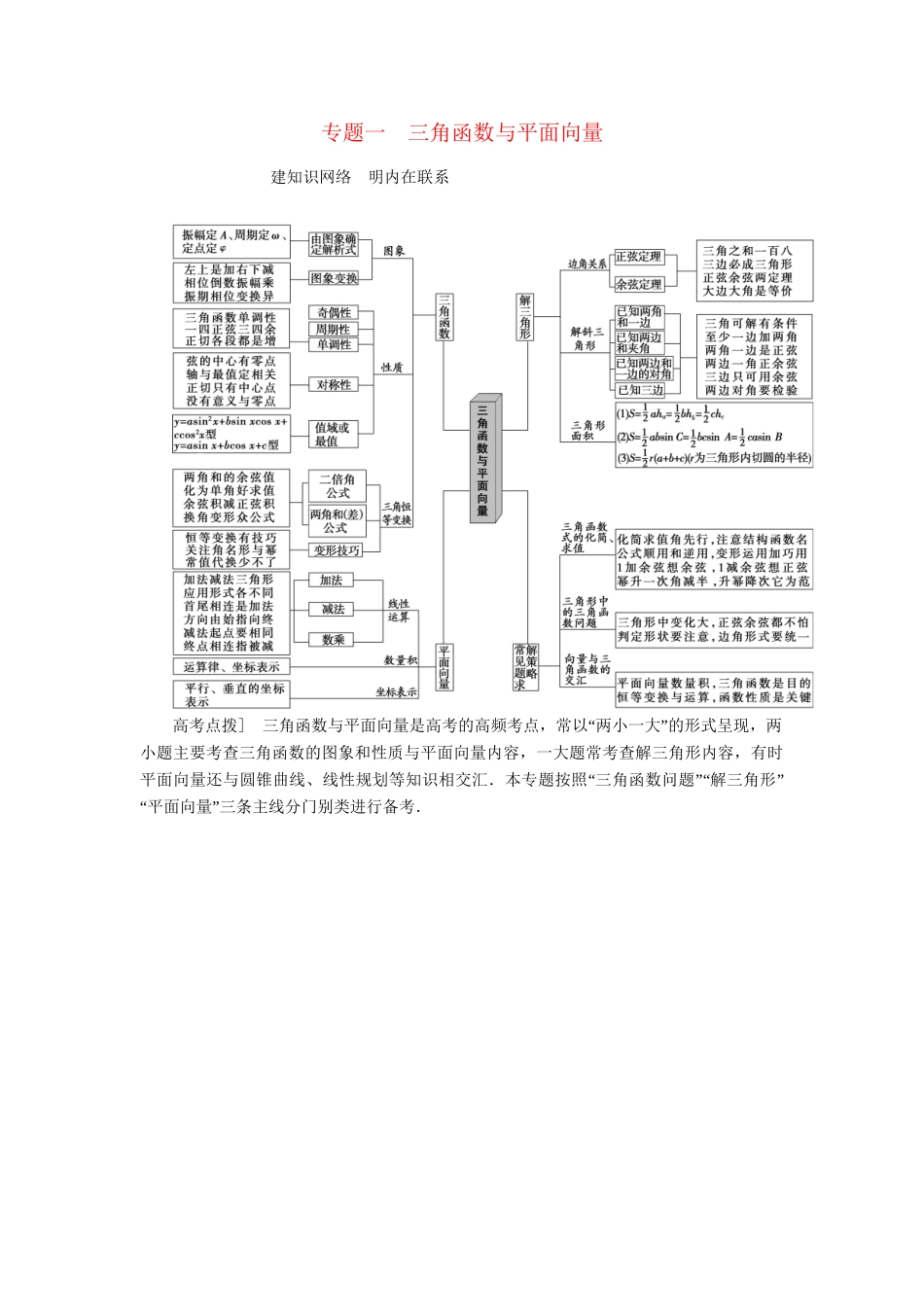
专题一三角函数与平面向量建知识网络明内在联系高考点拨]“”三角函数与平面向量是高考的高频考点,常以两小一大的形式呈现,两小题主要考查三角函数的图象和性质与平面向量内容,一大题常考查解三角形内容,有时“”“”平面向量还与圆锥曲线、线性规划等知识相交汇.本专题按照三角函数问题解三角形“”平面向量三条主线分门别类进行备考.突破点1三角函数问题提炼1三角函数的图象问题(1)函数y=Asin(ωx+φ)解析式的确定:利用函数图象的最高点和最低点确定A,利用周期确定ω,利用图象的某一已知点坐标确定φ.(2)三角函数图象的两种常见变换提炼2三角函数奇偶性与对称性(1)y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数;当φ=kπ+(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ+(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ,(k∈Z)解得.(2)y=Acos(ωx+φ),当φ=kπ+(k∈Z)时为奇函数;当φ=kπ(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ+(k∈Z)解得.y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数;对称中心的横坐标可由ωx+φ=(k∈Z)解得,无对称轴.提炼3三角变换常用技巧(1)“常值代换:特别是1”的代换,1=sin2θ+cos2θ=tan45°等.(2)项的分拆与角的配凑:如sin2α+2cos2α=(sin2α+cos2α)+cos2α,α=(α-β)+β等.(3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次.(4)弦、切互化:一般是切化弦.提炼4三角函数最值问题(1)y=asinx+bcosx+c型函数的最值:可将y转化为y=sin(x+φ)+c其中tanφ=的形式,这样通过引入辅助角φ可将此类函数的最值问题转化为y=sin(x+φ)+c的最值问题,然后利用三角函数的图象和性质求解.(2)y=asin2x+bsinxcosx+ccos2x型函数的最值:可利用降幂公式sin2x=,sinxcosx=,cos2x=,将y=asin2x+bsinxcosx+ccos2x转化整理为y=Asin2x+Bcos2x+C,这样就可将其转化为(1)的类型来求最值.回访1三角函数的图象问题1.(2016·全国甲卷)若将函数y=2sin2x的图象向左平移个单位长度,则平移后图象的对称轴为()A.x=-(k∈Z)B.x=+(k∈Z)C.x=-(k∈Z)D.x=+(k∈Z)B将函数y=2sin2x的图象向左平移个单位长度,得到函数y=2sin2=2sin的图象.由2x+=kx+(k∈Z),得x=+(k∈Z),即平移后图象的对称轴为x=+(k∈Z).]2.(2014·全国卷Ⅰ)图11如图11,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M.将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在0,π]的图象大致为()B如图所示,当x∈时,则P(cosx,sinx),M(cosx,0),作MM′⊥OP,M′为垂足,则=sinx,∴=sinx,∴f(x)=sinxcosx=sin2x,则当x=时,f(x)max=;当x∈时,有=sin(π-x),f(x)=-sinxcosx=-sin2x,当x=时,f(x)max=.只有B选项的图象符合.]回访2三角函数的性质问题3.(2015·全国卷Ⅰ)函数f(x)=cos(ωx+φ)的部分图象如图12所示,则f(x)的单调递减区间为()图12A.,k∈ZB.,k∈ZC.,k∈ZD.,k∈ZD由图象知,周期T=2=2,∴=2,∴ω=π.由π×+φ=+2kπ,k∈Z,不妨取φ=,∴f(x)=cos.由2kπ<πx+<2kπ+π,k∈Z,得2k-