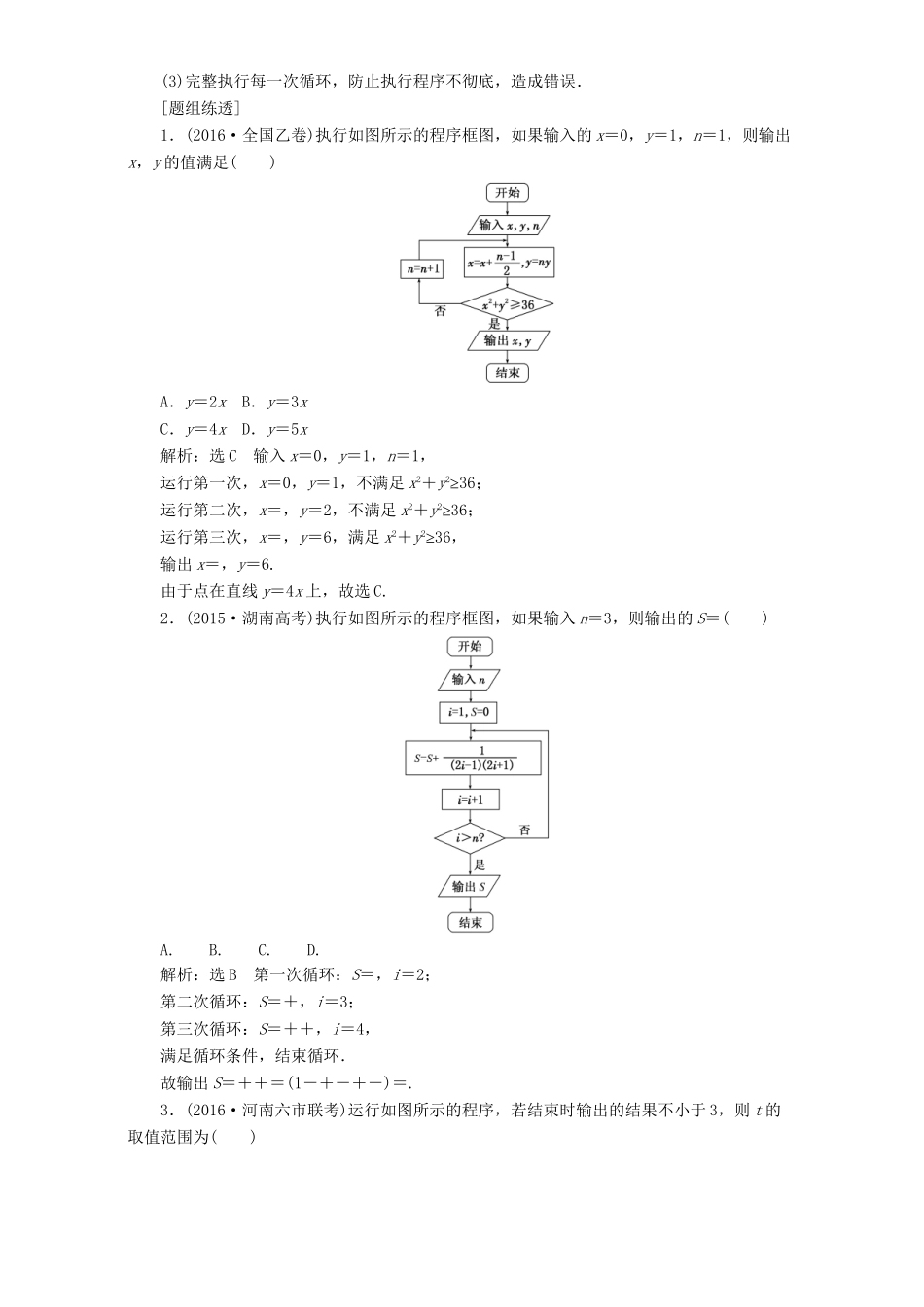
题型专题(六)算法、复数、推理与证明1.复数的除法复数的除法一般是先将分母实数化,即分子、分母同乘以分母的共轭复数再进一步化简.2.复数运算中常见的结论(1)(1±i)2=±2i,=i,=-i;(2)-b+ai=i(a+bi);(3)i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i;(4)i4n+i4n+1+i4n+2+i4n+3=0.[题组练透]1.(2016·全国丙卷)若z=1+2i,则=()A.1B.-1C.iD.-i解析:选C因为z=1+2i,则z=1-2i,所以=(1+2i)(1-2i)=5,则==i.故选C.2.(2016·广州模拟)已知复数z=,其中i为虚数单位,则复数z的共轭复数z所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限解析:选D z====1+2i,∴z=1-2i,∴z所对应的点(1,-2)在第四象限.3.(2016·武昌调研)已知(1+2i)z=4+3i(其中i是虚数单位,z是z的共轭复数),则z的虚部为()A.1B.-1C.iD.-i解析:选A因为z====2-i,所以z=2+i,故选A.4.(2016·河南六市联考)已知i为虚数单位,a∈R,若为纯虚数,则复数z=2a+i的模等于()A.B.C.D.解析:选C由题意得,=ti,t≠0,∴2-i=-t+tai,∴解得∴z=2a+i=1+i,|z|=,故选C.[技法融会]复数问题的解题思路(1)以复数的基本概念、几何意义、相等的条件为基础,结合四则运算,利用复数的代数形式列方程或方程组解决问题.(2)若与其他知识结合考查,则要借助其他的相关知识解决问题.利用循环结构表示算法要注意的3个问题(1)要选择准确的表示累计的变量;(2)要注意在哪一步结束循环;(3)完整执行每一次循环,防止执行程序不彻底,造成错误.[题组练透]1.(2016·全国乙卷)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()A.y=2xB.y=3xC.y=4xD.y=5x解析:选C输入x=0,y=1,n=1,运行第一次,x=0,y=1,不满足x2+y2≥36;运行第二次,x=,y=2,不满足x2+y2≥36;运行第三次,x=,y=6,满足x2+y2≥36,输出x=,y=6.由于点在直线y=4x上,故选C.2.(2015·湖南高考)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.解析:选B第一次循环:S=,i=2;第二次循环:S=+,i=3;第三次循环:S=++,i=4,满足循环条件,结束循环.故输出S=++=(1-+-+-)=.3.(2016·河南六市联考)运行如图所示的程序,若结束时输出的结果不小于3,则t的取值范围为()A.B.C.D.解析:选B依次运行程序框图中的语句可得,n=2,x=2t,a=1;n=4,x=4t,a=3;n=6,x=8t,a=3.此时结束循环,输出的ax=38t≥3,则8t≥1,t≥,故选B.4.(2016·河北五校联考)如图所示的程序框图输出的结果是S=720,则判断框内应填的是()A.i≤7B.i>7C.i≤9D.i>9解析:选B第一次运行,i=10,满足条件,S=1×10=10,i=9;第二次运行,i=9满足条件,S=10×9=90,i=8;第三次运行,i=8满足条件,S=90×8=720,i=7;此时不满足条件,输出的S=720.故条件应为i=8,9,10满足,i=7不满足,所以条件应为i>7.[技法融会]1.解答程序框图(流程图)问题的方法(1)首先要读懂程序框图,要熟练掌握程序框图的三种基本结构,特别是循环结构,在累加求和、累乘求积、多次输入等有规律的科学计算中,都有循环结构.(2)准确把握控制循环的变量,变量的初值和循环条件,弄清在哪一步结束循环;弄清循环体和输入条件、输出结果.(3)对于循环次数比较少的可逐步写出,对于循环次数较多的可先依次列出前几次循环结果,找出规律.2.(易错提醒)循环结构的两个注意点:(1)注意区分计数变量与循环变量.(2)注意哪一步结束循环.1.合情推理的解题思路(1)在进行归纳推理时,要先根据已知的部分个体,把它们适当变形,找出它们之间的联系,从而归纳出一般结论.(2)在进行类比推理时,要充分考虑已知对象性质的推理过程,然后通过类比,推导出类比对象的性质.(3)归纳推理关键是找规律,类比推理关键是看共性.2.类比推理和归纳推理在近几年高考题中未单独考查,学生在复习时,应重点关注归纳推理.[题组练透]1.如图,在平面直角坐标系的格点(横、纵坐标均为整数的点)处:点(1,0)处标b1,点(1,-1)处标b2,点(0,-...