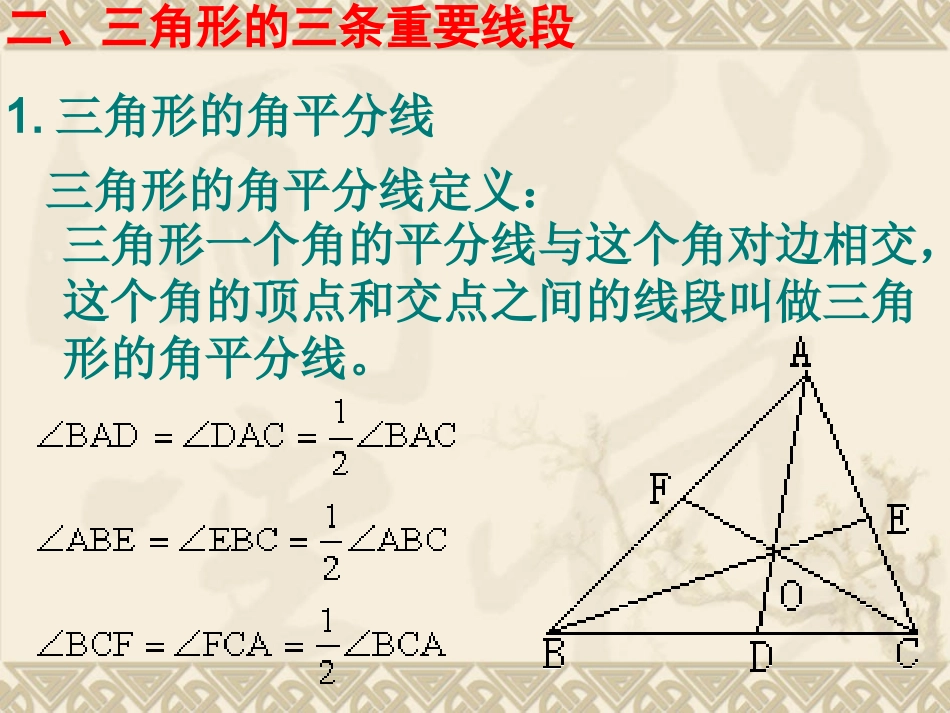
多边形的复习由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。一、三角形的概念三角形定义:请回答:(1)怎样表示出右图的三角形?说出它的顶点,内角,外角分别是什么?(2)角和边之间是什么关系?三角形一个角的平分线与这个角对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。二、三角形的三条重要线段1.三角形的角平分线三角形的角平分线定义:重要图形:在下列三角形ABC中,BO与CO分别是角平分线,∠BOC与∠A有何关系?图(1)图(2)图(3)例1如图1,点D是△ABC两个内角平分线的交点,证明:∠D=90°+A∠.证明: ∠1=∠,∠2=∠,∴21∠+22∠+∠A=180°①∠1+∠2+∠D=180°②①-2×②得:∠A-2∠D=-180°∠D=90°+A∠.点评利用角平分线的定义和三角形的内角和等于180°,不难证明.例2如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.证明:如图2: DB和DC是△ABC的两条外角平分线,∴∠D=180°-∠1-∠2=180°-(∠CBE+BCF∠)=180°-(∠A+4+A+3∠∠∠)=180°-(∠A+180°)=180°-∠A-90°=90°-∠A;点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.例3如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,证明:∠E=∠A.证明:如图3: ∠1=∠2,∠3=∠4,∠A+2∠1=2∠4①∠1+∠E=∠4②①×代入②得:∠E=∠A.点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.总结:以上3个例题都运用了三角形的角平分线、内角和,外角的性质以及方程思想。2.三角形的中线三角形的中线定义:二、三角形的三条重要线段在三角形中,连结一个顶点和它的对边中点的线段,叫做三角形的中线。如图,AD是三角形ABC的中线,则三角形ABD与三角形ADC的面积关系如何?周长关系呢?应用从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高。3.三角形的高三角形的高定义:二、三角形的三条重要线段注意:三角形的角平分线,中线和高都是线段,在画图时不能画成直线,射线。三、三角形三条边的关系定理:三角形两边之和大于第三边,三角形两边之差小于第三边。abc1.三角形内角和定理:四、三角形的内角和三角形三个内角的和等于180°。方法一:如图,过△ABC中的顶点A作EF//BC。如何理解这个定理?方法二:如图,延长△ABC中的BC到D,过C点作CE//AB。(1)直角三角形的两个锐角互余:如图在△ABC中,∠C=90°那么∠A+∠B=90°2.三角形内角和定理推论(2)三角形的一个外角等于和它不相邻的两个内角的和。即:如图∠ACD是△ABC的一个外角,那么∠ACD=∠A+∠B。如图:AD与BC相交于点O,则∠A+∠C=∠B+∠D。ABCD如图:∠BDC=∠B+∠A+∠CBACD(3)三角形的一个外角大于任何一个和它不相邻的内角。即:如图∠ACD是△ABC的一个外角,那么∠ACD>∠A,∠ACD>∠B。注意:三角形的任何一个外角与相邻内角是邻补角,与不相邻的两个内角和相等且大于任何一个不相邻的内角。应用时要搞清楚外角与内角的位置关系,正确运用。ABC如图:CD是三角形ABC的外角平分线,证明:∠BAC>∠B.证明: ∠BAC是△ACD的外角∴∠BAC>∠ACD ∠DCE是△BCD的外角∴∠DCE>∠B CD是∠ACB的平分线∴∠ACD=∠DCE∴∠BAC>B.∠点评:本例主要利用了三角形的外角的性质,应用时要搞清楚外角与内角的位置关系,正确运用。过n边形一个顶点连对角线,可以得(n-3)条对角线,并且将n边形分成(n-2)个三角形,这(n-2)个三角形的内角和恰好是多边形的内角和,等于(n-2)·180°。五、多边形内角和定理六、多边形的外角和定理1、多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°,外角和等于n·180°-(n-2)·180°=360°14322、多边形外角和定理:任意多边形的外角和等于360°.注意:n边形的外角和恒等于360°,它与边数的多少无关.3、多边形最多有三个内角为锐角,最少没有锐角(如矩形);多边形的外角中最多有三个钝角,最少没有钝角。七、用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一...