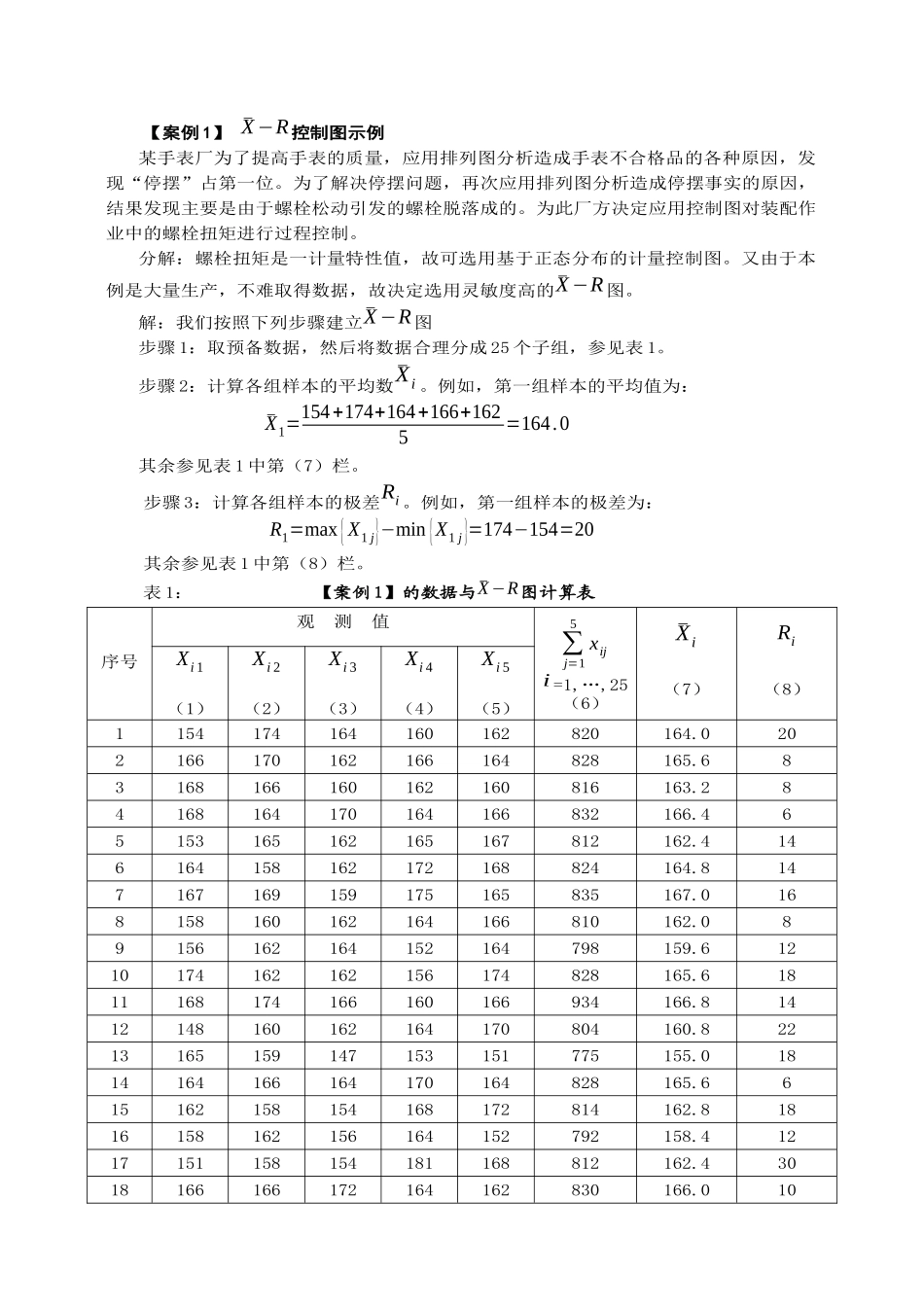
CLLCLUCL质量特性样本号统计过程控制(SPC)案例分析一、用途1.分析判断生产过程的稳定性,生产过程处于统计控制状态。2.及时发现生产过程中的异常现象和缓慢变异,预防不合格品产生。3.查明生产设备和工艺装备的实际精度,以便作出正确的技术决定。4.为评定产品质量提供依据。二、控制图的基本格式1.标题部分X-R控制图数据表产品名称工作指令编号收集数据期间质量特性车间观察方法规定日产量设备编号规格界限(或要求)Tu抽样间隔操作人员TL数量作业指导书编号仪器编号检验人员生产过程质量要求日期时间样本号测定值均值¯X极差R备注X1X2X3X4X5计算:¯X图:CL=¯¯XR图:CL=¯RUCL=¯¯X+A2¯RUCL=D4¯RLCL=¯¯X-A2¯RLCL=D3¯R2.控制图部分在方格纸上作出控制图:¯X−R控制图¯X图R图说明操作人班组长质量工程师横坐标为样本序号,纵坐标为产品质量特性。图上有三条平行线:实线CL:中心线虚线UCL:上控制界限线LCL:下控制界限线。三、控制图的设计原理1.正态性假设:绝大多数质量特性值服从或近似服从正态分布。2.3σ准则:99.73%。3.小概率事件原理:小概率事件一般是不会发生的。4.反证法思想。四、控制图的种类1.按产品质量的特性分:(1)计量值(¯X−R,~X−R,X−RS,¯X−S)(2)计数值(p,pn,u,c图)。2.按控制图的用途分:(1)分析用控制图;(2)控制用控制图。五、控制图的判断规则1.分析用控制图:规则1判稳准则——绝大多数点子在控制界限线内(3种情况);规则2判异准则——排列无下述现象(8种情况)。2.控制用控制图:规则1每一个点子均落在控制界限内。规则2控制界限内点子的排列无异常现象。【案例1】¯X−R控制图示例某手表厂为了提高手表的质量,应用排列图分析造成手表不合格品的各种原因,发现“停摆”占第一位。为了解决停摆问题,再次应用排列图分析造成停摆事实的原因,结果发现主要是由于螺栓松动引发的螺栓脱落成的。为此厂方决定应用控制图对装配作业中的螺栓扭矩进行过程控制。分解:螺栓扭矩是一计量特性值,故可选用基于正态分布的计量控制图。又由于本例是大量生产,不难取得数据,故决定选用灵敏度高的¯X−R图。解:我们按照下列步骤建立¯X−R图步骤1:取预备数据,然后将数据合理分成25个子组,参见表1。步骤2:计算各组样本的平均数¯Xi。例如,第一组样本的平均值为:¯X1=154+174+164+166+1625=164.0其余参见表1中第(7)栏。步骤3:计算各组样本的极差Ri。例如,第一组样本的极差为:R1=max{X1j}−min{X1j}=174−154=20其余参见表1中第(8)栏。表1:【案例1】的数据与¯X−R图计算表序号观测值∑j=15xiji=1,…,25(6)¯Xi(7)Ri(8)Xi1(1)Xi2(2)Xi3(3)Xi4(4)Xi5(5)1154174164160162820164.0202166170162166164828165.683168166160162160816163.284168164170164166832166.465153165162165167812162.4146164158162172168824164.8147167169159175165835167.0168158160162164166810162.089156162164152164798159.61210174162162156174828165.61811168174166160166934166.81412148160162164170804160.82213165159147153151775155.01814164166164170164828165.6615162158154168172814162.81816158162156164152792158.41217151158154181168812162.43018166166172164162830166.01013579111315171921232530.18814.2800.000135791113151719212325171.512163.272155.032序号观测值∑j=15xiji=1,…,25(6)¯Xi(7)Ri(8)Xi1(1)Xi2(2)Xi3(3)Xi4(4)Xi5(5)19170170166160160826165.21020168160162154160804160.81421162164165169153813162.61622166160170172158826165.21423172164159167160822164.41324174164166157162823164.61725151160164158170803160.619步骤4:计算样本总均值¯¯X与平均样本极差¯R。由于∑¯Xi=4081.8,∑R=357,故:¯¯X=163.272,¯R=14.280。步骤5:计算R图的参数。先计算R图的参数。从D3、D4系数表可知,当子组大小n=5,D4=2.114,D3=0,代入R图的公式,得到:UCLR=D4¯R=2.114×14.280=30.188CLR=¯R=14.280LCLR=D3¯R=—极差控制图:均值控制图:图1【案例1】的第一次...