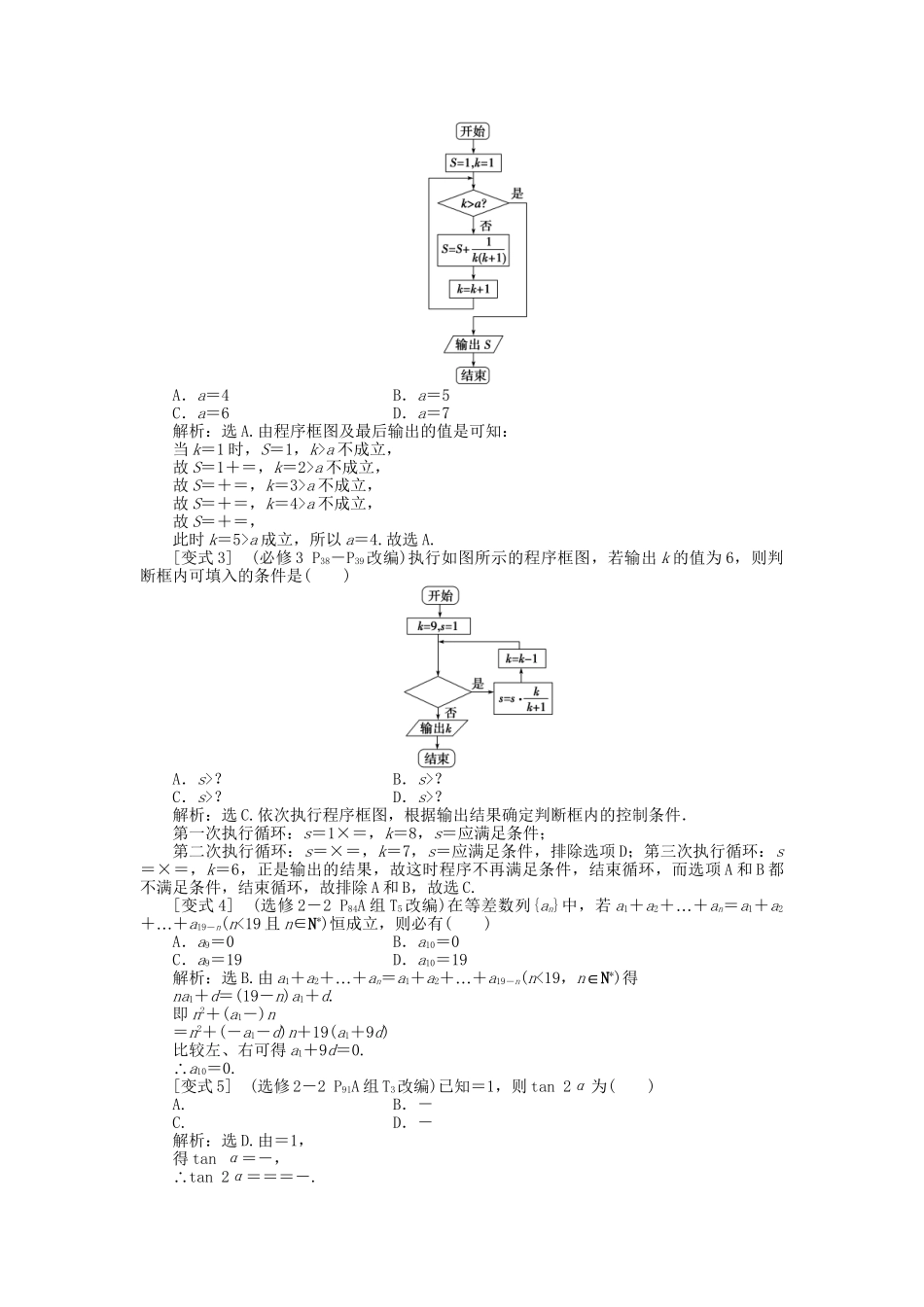
(通用版)2016年高考数学二轮复习专题十二推理与证明、算法初步考题溯源教材变式理真题示例对应教材题材评说(2014·高考课标全国卷Ⅱ,5分)数列{an}满足an+1=,a8=2,则a1=________.(2015·高考全国卷Ⅱ,5分)下边程序框图的算法思路源于我国古代数学名著《九“章算术》中的更相减损”术.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4D.14(2015·高考全国卷Ⅱ,5分)设Sn是数列{an}的前n项和,且a1=-1,an+1=SnSn+1,则Sn=________.(必修5P33A组T4(2))已知数列{an}中,a1=-,an=1-(n>1),写出数列的前5项.(必修3P36例1)用更相减损术求98与63的最大公约数.(选修2-2P84B组T1)已知数列{an}的前n项和为Sn,a1=-,满足Sn++2=an(n≥2),计算S1,S2,S3,S4,并猜想Sn的表达式.考题与教材题形同孪生姐妹,正向逆向结合是殊途同归的典型.[教材变式训练]一、选择题[变式1](选修2-2P77练习T2改编)观察三角数阵,记第n行的第m个数为a(n,m),则下列关系正确的是()111121133114641…11045…45101A.a(n+1,m+1)=a(n,m)+a(n,m+1)B.a(n+1,m+1)=a(n-1,m-1)+a(n,m)C.a(n+1,m+1)=a(n,m)+a(n+1,m)D.a(n+1,m+1)=a(n+1,m)+a(n,m+1)解析:选A.“”观察分析得出三角数阵中的每一个数等于其肩上两个数之和.∴a(n+1,m+1)=a(n,m)+a(n,m+1).[变式2](必修3P13例6改编)程序框图如图所示,若该程序运行后输出的值是,则()A.a=4B.a=5C.a=6D.a=7解析:选A.由程序框图及最后输出的值是可知:当k=1时,S=1,k>a不成立,故S=1+=,k=2>a不成立,故S=+=,k=3>a不成立,故S=+=,k=4>a不成立,故S=+=,此时k=5>a成立,所以a=4.故选A.[变式3](必修3P38-P39改编)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是()A.s>?B.s>?C.s>?D.s>?解析:选C.依次执行程序框图,根据输出结果确定判断框内的控制条件.第一次执行循环:s=1×=,k=8,s=应满足条件;第二次执行循环:s=×=,k=7,s=应满足条件,排除选项D;第三次执行循环:s=×=,k=6,正是输出的结果,故这时程序不再满足条件,结束循环,而选项A和B都不满足条件,结束循环,故排除A和B,故选C.[变式4](选修2-2P84A组T5改编)在等差数列{an}中,若a1+a2…++an=a1+a2…++a19-n(n<19且n∈N*)恒成立,则必有()A.a9=0B.a10=0C.a9=19D.a10=19解析:选B.由a1+a2…++an=a1+a2…++a19-n(n<19,n∈N*)得na1+d=(19-n)a1+d.即n2+(a1-)n=n2+(-a1-d)n+19(a1+9d)比较左、右可得a1+9d=0.∴a10=0.[变式5](选修2-2P91A组T3改编)已知=1,则tan2α为()A.B.-C.D.-解析:选D.由=1,得tanα=-,∴tan2α===-.[变式6](选修2-2P98A组T2改编)等于()A.3nB.×9nC.(10n-1)D.1+2n解析:选C.法一:当n=1时,原式==3,A,B,C,D均满足,当=2时,原式===33,仅有C满足.法二: 个=1+10+102…++102n-1==(102n-1),个=2(1+10+102…++10n-1)=2·=(10n-1),====(10n-1).二、填空题[变式7](选修2-2P71例1改编)在数列{an}中,an+1=,a10=,则a1=________.解析:对于{an}, an+1=,∴=+1,∴是以为首项,1为公差的等差数列.∴=+9,∴=+9,∴a1=2.答案:2[变式8](选修2-2P84B组T1改编)已知数列{an}的前n项和为Sn,a1=-,且Sn++2=an(n≥2),猜想Sn=________.解: a1=-,Sn++2=an,∴S1=a1=-.又S2++2=a2=S2-S1=S2+,∴S2=-,又S3++2=a3=S3-S2=S3+,∴S3=-.所以猜想Sn=-.答案:-三、解答题[变式9](选修2-2P84A组T4改编)在△ABC中,内角A、B、C有关系++≥.在四边形ABCD中,内角A、B、C、D有关系+++≥.在五边形ABCDE中,内角A、B、C、D、E有关系++++≥.(1)猜想在n边形A1A2…An中有怎样的关系;(2)用你学过的知识,证明△ABC中的关系++≥.解:(1)…观察规律:+++≥.(2)证明: 在△ABC中,A+B+C=π,∴(A+B+C)=3++++++≥3+2+2+2=9,当且仅当A=B=C=时,等号成立...