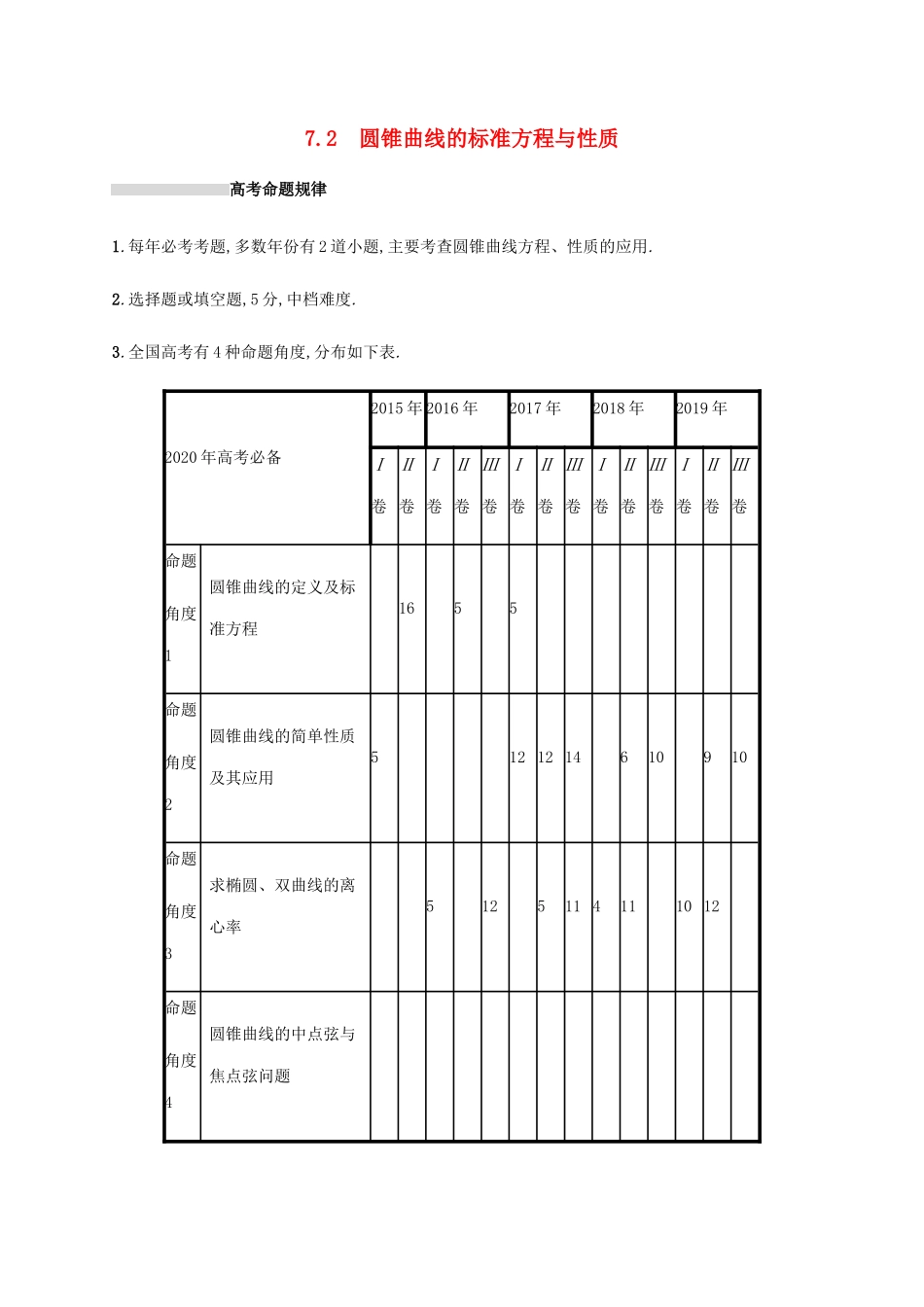
7.2圆锥曲线的标准方程与性质高考命题规律1.每年必考考题,多数年份有2道小题,主要考查圆锥曲线方程、性质的应用.2.选择题或填空题,5分,中档难度.3.全国高考有4种命题角度,分布如下表.2020年高考必备2015年2016年2017年2018年2019年Ⅰ卷Ⅱ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷命题角度1圆锥曲线的定义及标准方程1655命题角度2圆锥曲线的简单性质及其应用5121214610910命题角度3求椭圆、双曲线的离心率5125114111012命题角度4圆锥曲线的中点弦与焦点弦问题命题角度1圆锥曲线的定义及标准方程高考真题体验·对方向1.(2017全国Ⅰ·5)已知F是双曲线C:x2-y23=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为()A.13B.12C.23D.32答案D解析由c2=a2+b2=4,得c=2,所以点F的坐标为(2,0).将x=2代入x2-y23=1,得y=±3,所以PF=3.又点A的坐标是(1,3),故△APF的面积为12×3×(2-1)=32,故选D.2.(2016全国Ⅱ·5)设F为抛物线C:y2=4x的焦点,曲线y=kx(k>0)与C交于点P,PF⊥x轴,则k=()A.12B.1C.32D.2答案D解析因为F为抛物线y2=4x的焦点,所以F(1,0).又因为曲线y=kx(k>0)与抛物线交于点P,PF⊥x轴,如图所示,可知P(1,2),故k1=2,解得k=2,故选D.3.(2017北京·10)若双曲线x2-y2m=1的离心率为❑√3,则实数m=.答案2解析由题意知a=1,b=❑√m,m>0,c=❑√a2+b2=❑√1+m,则离心率e=ca=❑√1+m=❑√3,解得m=2.4.(2016山东·14)已知双曲线E:x2a2−y2b2=1(a>0,b>0).矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是.答案2解析由题意不妨设AB=3,则BC=2.设AB,CD的中点分别为M,N,如图,则在Rt△BMN中,MN=2,故BN=❑√BM2+MN2=❑√(32)2+22=52.由双曲线的定义可得2a=BN-BM=52−32=1,而2c=MN=2,所以双曲线的离心率e=2c2a=2.典题演练提能·刷高分1.已知椭圆C:x2a2+y2b2=1(a>b>0),若长轴长为6,且两焦点恰好将长轴三等分,则此椭圆的标准方程为()A.x236+y232=1B.x29+y28=1C.x29+y25=1D.x216+y212=1答案B解析 椭圆长轴长为6,焦点恰好将长轴三等分,∴2a=6,a=3,∴6c=6,c=1,b2=a2-1=8,∴椭圆方程为x29+y28=1,故选B.2.已知F为抛物线C:y2=4x的焦点,过点F的直线l交抛物线C于A,B两点,若|AB|=8,则线段AB的中点M到直线x+1=0的距离为()A.2B.4C.8D.16答案B解析如图,抛物线y2=4x的焦点为F(1,0),准线为x=-1,即x+1=0,分别过A,B作准线的垂线,垂足为C,D,则有|AB|=|AF|+|BF|=|AC|+|BD|=8,过AB的中点M作准线的垂线,垂足为N,则MN为直角梯形ABDC的中位线,则|MN|=12(|AC|+|BD|)=4,即M到准线x=-1的距离为4.故选B.3.已知双曲线C:x2a2−y2b2=1(a>0,b>0)过点(❑√2,❑√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,则双曲线C的标准方程是()A.x212-y2=1B.x29−y23=1C.x2-y23=1D.x223−y232=1答案C解析由双曲线C:x2a2−y2b2=1(a>0,b>0)过点(❑√2,❑√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,可得{2a2-3b2=1,ba=❑√3,解得{a=1,b=❑√3,∴双曲线C的标准方程是x2-y23=1.故选C.4.已知点A(-1,0),B(1,0)为双曲线x2a2−y2b2=1(a>0,b>0)的左、右焦点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的方程为()A.x2-y24=1B.x2-y2=1C.x2-y23=1D.x2-y22=1答案B解析由点M在双曲线上,△ABM为等腰三角形,且顶角为120°,得|AB|=|BM|,∠ABM=120°,过点M作MN⊥x轴,垂足为N,则∠NBM=60°,如图所示.在Rt△BNM中,|BM|=|AB|=2a,∠NBM=60°,则|BN|=2acos60°=a,|MN|=2asin60°=❑√3a,即M(2a,❑√3a),代入双曲线方程得4-3a2b2=1,即b2=a2. 点A(-1,0),B(1,0)为双曲线的左、右顶点,∴a=b=1,∴双曲线的方程为x2-y2=1.5.已知抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB=60°.设线段AB的中点M在l上的投影为N,则()A.|AB|≥2|MN|B.2|AB|≥3|MN|C.|AB|≥3|MN|D.|AB|≥|MN|答案D解析由抛物线定义得|AF|+|BF|=2|MN|,在△AFB中,|AB|2=|AF|2+|BF|2-2|AF|·|BF|cos60°=|AF|2+|BF|2-|AF|·|BF|=(|AF|+|BF|)2-3|AF|·|BF|≥(|AF|+|BF|)2-3×(|AF|+|BF|2)2=(|AF|+|BF|)24=|MN|2,所以|AB|≥|MN|,故选D.6.已知抛物线C:y2=8x上一点P,直线l1:x=-2,l2:3x-5y+30=0,则...