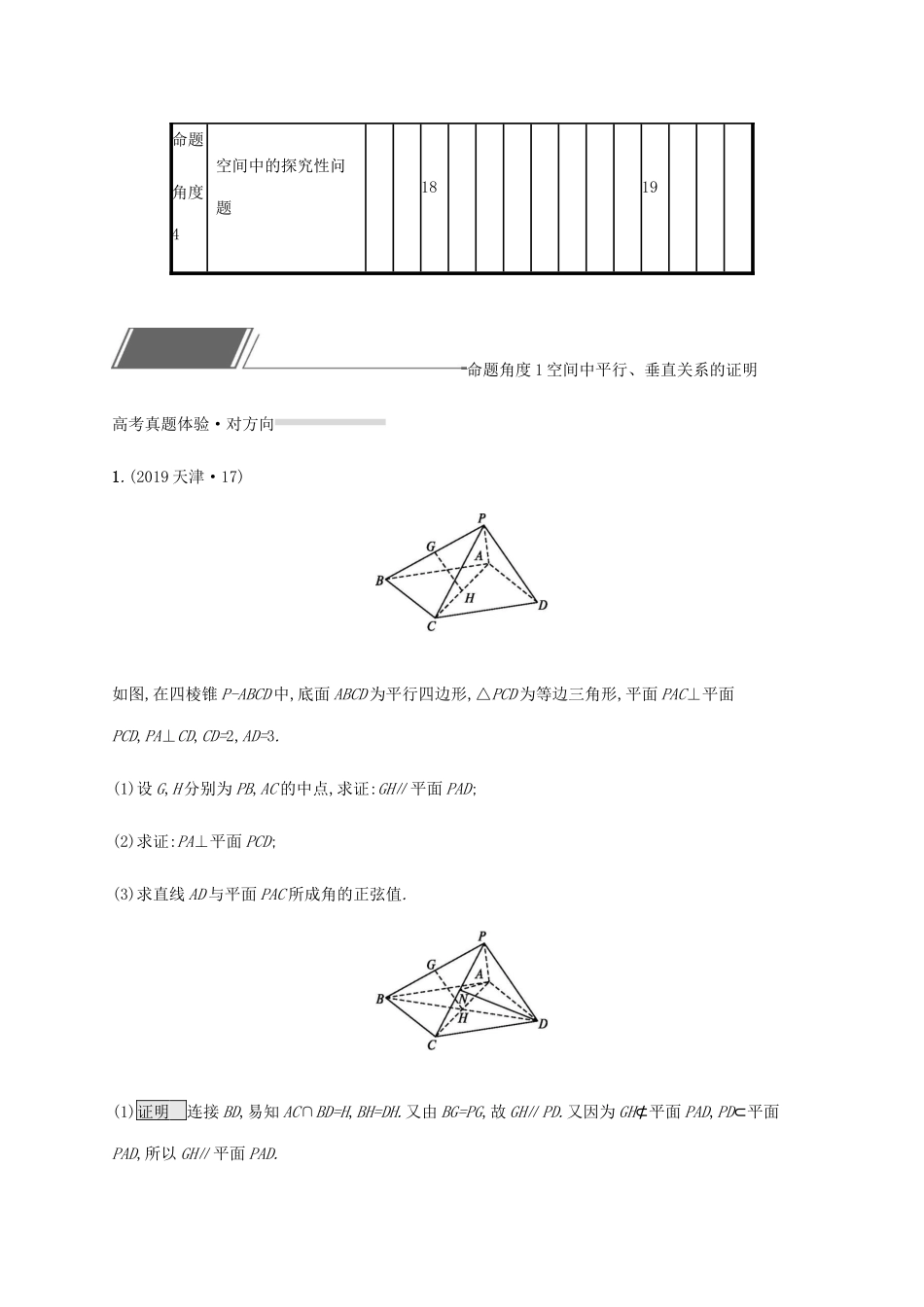
5.3立体几何解答题高考命题规律1.高考必考考题.主要以多面体为载体,考查空间位置关系的判定与性质、求几何体的体积、面积、距离等.2.解答题,12分,中等难度.3.全国高考有4种命题角度,分布如下表.2020年高考必备2015年2016年2017年2018年2019年Ⅰ卷Ⅱ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷命题角度1空间中平行、垂直关系的证明命题角度2几何体的体积与距离问题181919181818191917命题角度3空间中的折叠问题191819命题角度4空间中的探究性问题1819命题角度1空间中平行、垂直关系的证明高考真题体验·对方向1.(2019天津·17)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;(2)求证:PA⊥平面PCD;(3)求直线AD与平面PAC所成角的正弦值.(1)证明连接BD,易知AC∩BD=H,BH=DH.又由BG=PG,故GH∥PD.又因为GH⊄平面PAD,PD⊂平面PAD,所以GH∥平面PAD.(2)证明取棱PC的中点N,连接DN,依题意,得DN⊥PC,又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,所以DN⊥平面PAC,又PA⊂平面PAC,故DN⊥PA.又已知PA⊥CD,CD∩DN=D,所以PA⊥平面PCD.(3)解连接AN,由(2)中DN⊥平面PAC,可知∠DAN为直线AD与平面PAC所成的角.因为△PCD为等边三角形,CD=2且N为PC的中点,所以DN=❑√3,又DN⊥AN,在Rt△AND中,sin∠DAN=DNAD=❑√33.所以,直线AD与平面PAC所成角的正弦值为❑√33.2.(2017山东·18)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.证明(1)取B1D1的中点O1,连接CO1,A1O1,由于ABCD-A1B1C1D1是四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C.又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,又A1E⊥平面ABCD,BD⊂平面ABCD.所以A1E⊥BD,因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1.又A1E,EM⊂平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM,又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1.典题演练提能·刷高分1.如图,在三棱柱ABC-A1B1C1中,AB=AC,点E,F分别在棱BB1,CC1上(均异于端点),且∠ABE=∠ACF,AE⊥BB1,AF⊥CC1.求证:(1)平面AEF⊥平面BB1C1C;(2)BC∥平面AEF.证明(1)在三棱柱ABC-A1B1C1中,BB1∥CC1. AF⊥CC1,∴AF⊥BB1.又 AE⊥BB1,AE∩AF=A,AE,AF⊂平面AEF,∴BB1⊥平面AEF,又 BB1⊂平面BB1C1C,∴平面AEF⊥平面BB1C1C.(2) AE⊥BB1,AF⊥CC1,∠ABE=∠ACF,AB=AC,∴Rt△AEB≌Rt△AFC,∴BE=CF,又由(1)知,BE∥CF.∴四边形BEFC是平行四边形,从而BC∥EF.又 BC⊄平面AEF,EF⊂平面AEF,∴BC∥平面AEF.2.(2019四川成都一模)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,点M是棱PC的中点.(1)证明:PA∥平面BMD;(2)当PA=❑√3时,求三棱锥M-PAD的体积.(1)证明如图,连接AC交BD于点O,连接MO. M,O分别为PC,AC的中点,∴PA∥MO. PA⊄平面BMD,MO⊂平面BMD,∴PA∥平面BMD.(2)解如图,取线段BC的中点H,连接AH. 四边形ABCD是菱形,∠ABC=60°,∴AH⊥AD. PA⊥平面ABCD,∴AH⊥PA.又PA∩AD=A,所以AH⊥平面PAD,∴点H到平面PAD的距离即为AH的长度.又BC∥AD,∴点C到平面PAD的距离即为AH的长度. M为PC的中点,∴点M到平面PAD的距离即为12AH的长度.∴VM-PAD=13S△PAD·12AH=12×13×12×❑√3×2×❑√3=12.3.如图,在直角△ABC中,∠ACB=90°,BC=2AC=4,D,E分别是AB,BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.(1)求四棱锥F-ACED的体积;(2)求证:平面ADF⊥平面ACF.(1)解 D,E分别是AB,BC边的中点,∴DE平行且等于AC的一半,DE⊥BC,DE=1.依题意,DE⊥EF,BE=EF=2.于是有DE⊥BCDE⊥EFEF⋂EC=EEF,EC⊂平面CEF}⇒DE⊥平面CEF. DE⊥平面CEF,∴平面ACED⊥平面CEF.过F点作FM⊥EC于点M,则平面ACED⊥平面CEF,且交线为CEFM⊥ECFM⊂平面CEF}⇒FM⊥平面ACED, ∠CEF=60°,∴FM=❑√3,∴梯形ACED的面积S=12(AC+ED)×EC=12×(1+2)×2=3,∴四棱锥F-ACED的体积V=13Sh=13×3×❑√3=❑√3.(2)证明如图,设线...