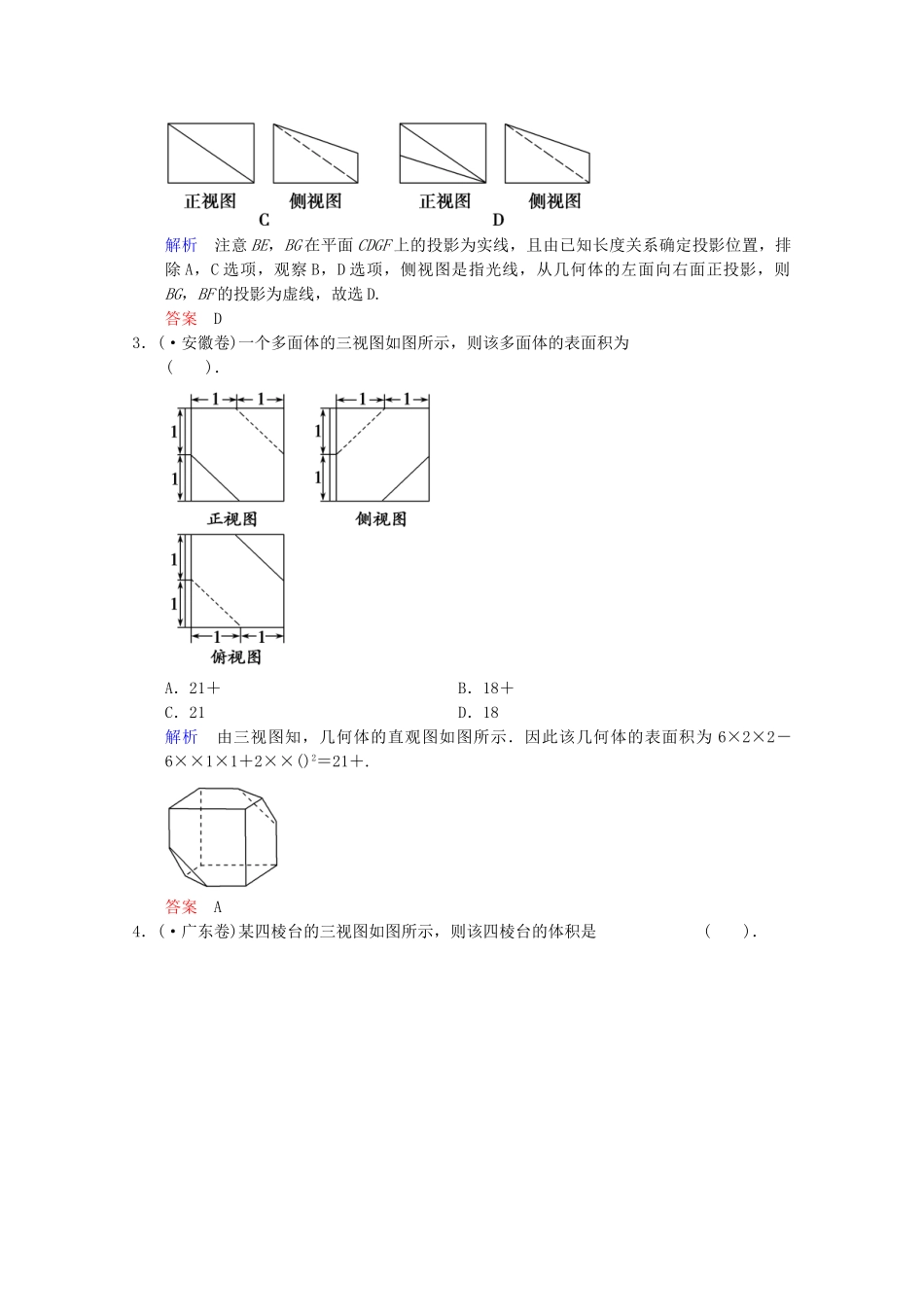
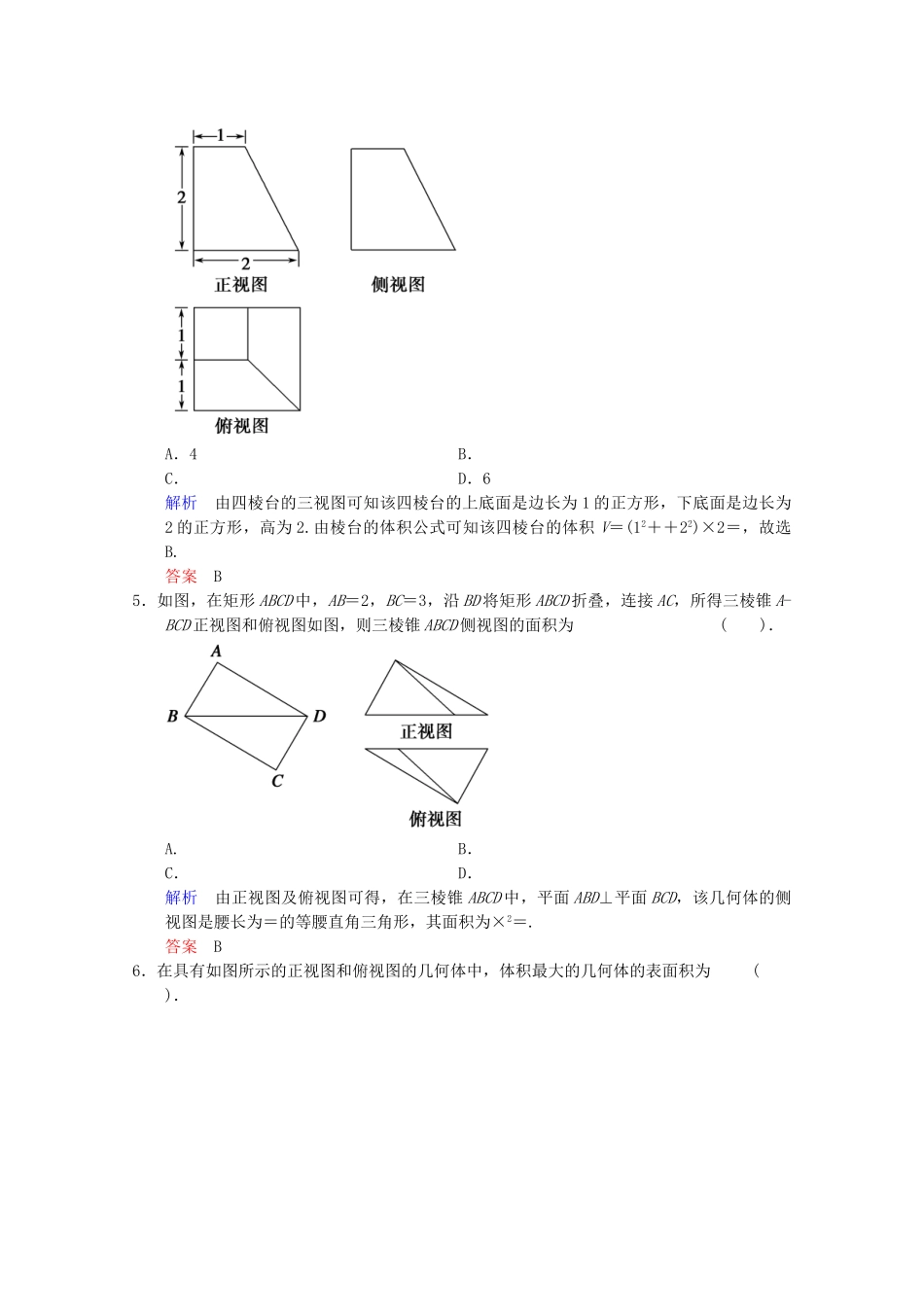
专题四立体几何第1讲三视图及空间几何体的计算问题(建议用时:60分钟)一、选择题1.(·湖北卷)在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①②③④的四个图,则该四面体的正视图和俯视图分别为().A.①和②B.③和①C.④和③D.④和②解析由三视图可知,该几何体的正视图是一个直角三角形,三个顶点的坐标分别是(0,0,2),(0,2,0),(0,2,2)且内有一个虚线(一个顶点与另一直角边中点的连线),故正视图是④;俯视图即在底面的射影是一个斜三角形,三个顶点的坐标分别是(0,0,0),(2,2,0),(1,2,0),故俯视图是②.答案D2.(·东北三校第三次模拟)如图,多面体ABCDEFG的底面ABCD为正方形,FC=GD=2EA,其俯视图如下,则其正视图和侧视图正确的是().解析注意BE,BG在平面CDGF上的投影为实线,且由已知长度关系确定投影位置,排除A,C选项,观察B,D选项,侧视图是指光线,从几何体的左面向右面正投影,则BG,BF的投影为虚线,故选D.答案D3.(·安徽卷)一个多面体的三视图如图所示,则该多面体的表面积为().A.21+B.18+C.21D.18解析由三视图知,几何体的直观图如图所示.因此该几何体的表面积为6×2×2-6××1×1+2××()2=21+.答案A4.(·广东卷)某四棱台的三视图如图所示,则该四棱台的体积是().A.4B.C.D.6解析由四棱台的三视图可知该四棱台的上底面是边长为1的正方形,下底面是边长为2的正方形,高为2.由棱台的体积公式可知该四棱台的体积V=(12++22)×2=,故选B.答案B5.如图,在矩形ABCD中,AB=2,BC=3,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD正视图和俯视图如图,则三棱锥ABCD侧视图的面积为().A.B.C.D.解析由正视图及俯视图可得,在三棱锥ABCD中,平面ABD⊥平面BCD,该几何体的侧视图是腰长为=的等腰直角三角形,其面积为×2=.答案B6.在具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为().A.13B.7+3C.πD.14解析由正视图和俯视图可知,该几何体可能是四棱柱或者是水平放置的三棱柱或水平放置的圆柱.由图象可知四棱柱的体积最大.四棱柱的高为1,底面边长分别为1,3,所以表面积为2(1×3+1×1+3×1)=14.答案D7.(·湖南卷)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于().A.B.1C.D.解析易知正方体是水平放置的,又侧视图是面积为的矩形.所以正方体的对角面平行于投影面,此时正视图和侧视图相同,面积为.答案D二、填空题8.某几何体的三视图如图所示,则该几何体的体积为____________.解析由三视图可知该几何体由长方体和圆柱的一半组成.其中长方体的长、宽、高分别为4,2,2,圆柱的底面半径为2,高为4.所以V=2×2×4+×22×π×4=16+8π.答案16+8π9.(·江苏卷)如图,在三棱柱A1B1C1ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥FADE的体积为V1,三棱柱A1B1C1ABC的体积为V2,则V1∶V2=________.解析设三棱柱A1B1C1-ABC的高为h,底面三角形ABC的面积为S,则V1=×S·h=Sh=V2,即V1∶V2=1∶24.答案1∶2410.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.解析利用三棱锥的体积公式直接求解.VD1-EDF=VF-DD1F=S△D1DE·AB=××1×1×1=.答案11.(·重庆卷改编)某几何体的三视图如图所示,则该几何体的表面积为________.解析由俯视图可以判断该几何体的底面为直角三角形,由正视图和侧视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的.在长方体中分析还原,如图(1)所示,故该几何体的直观图如图(2)所示.在图(1)中,直角梯形ABPA1的面积为×(2+5)×4=14,计算可得A1P=5.直角梯形BCC1P的面积为×(2+5)×5=.因为A1C1⊥平面A1ABP,A1P⊂平面A1ABP,所以A1C1⊥A1P,故Rt△A1PC1的面积为×5×3=.又Rt△ABC的面积为×4×3=6,矩形ACC1A1的面积为5×3=15,故几何体ABC-A1PC1的表面积为14+++6+15=60.答案6012.已知三棱锥SABC的所有顶点都在球O的球面上,△A...