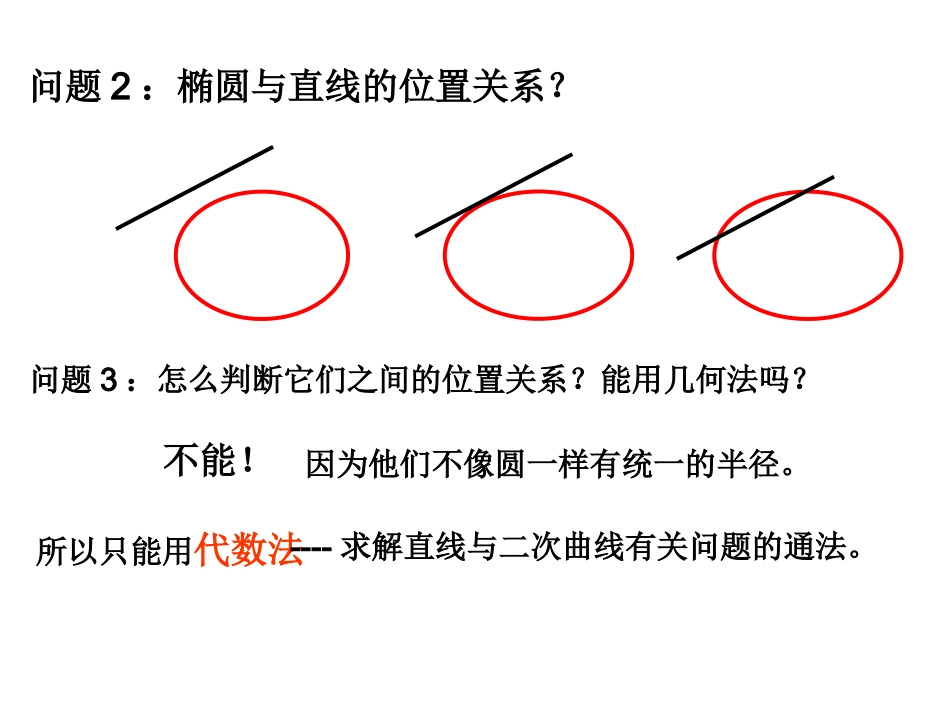
直线与椭圆的位置关系怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>rd0∆<0∆=0几何法:代数法:问题3:怎么判断它们之间的位置关系?能用几何法吗?问题2:椭圆与直线的位置关系?不能!所以只能用代数法----求解直线与二次曲线有关问题的通法。因为他们不像圆一样有统一的半径。直线与椭圆的位置关系的判定代数方法222201AxByCxyab由方程组20(0)mxnxpm24nmp△=0△0△=0△方程组有两解两个交点相交方程组有一解一个交点相切方程组无解无交点相离关于弦长计算:直线与二次曲线相交所得的弦长直线具有斜率k,直线与二次曲线的两个交点坐标分别为1122(,),(,)AxyBxy,则它的弦长2122124)(1xxxxkAB=2122124)(11yyyyk当直线斜率不存在时,则12AByy.例1、已知直线y=x-与椭圆x2+4y2=2,①判断它们的位置关系。2121xyx2+4y2=2解:联立方程组消去y01452xx∆>0因为所以方程(1)有两个根,则原方程组有两组解,直线与椭圆相交-----(1)例题讲解②求直线被椭圆所截的弦长|AB|.12124515xxxx由弦长公式得:2221212121(1)()4ABxxxxxxkk练习1:已知斜率为1的直线L过椭圆的右焦点,交椭圆于A,B两点,求弦AB之长.练习2:已知椭圆及直线,当直线和椭圆有公共点时,求实数的范围。1422yxkxyk1、判断直线与椭圆位置关系的方法:解方程组消去其中一元得一元二次型方程△<0相离△=0相切△>0相交小结2122124)(1xxxxkAB2、弦长公式:),(),,(2211yxByxA已知2122124)(11yyyyk例2:《P26例4》已知椭圆过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造P(2,m)变式:已知椭圆与直线l交于A、B两点,且弦AB的中点P的横坐标为2,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造练习2:椭圆19422yx的弦被点P(2,1)所平分,求此弦所在的直线方程。02029yx练习2.中心在原点一个焦点为的椭圆截直线所得弦的中点横坐标为,求椭圆的方程.23xy21)50,0(1F1257522xy221.()114425.xyPxyuxy例已知,是椭圆上的点,求的取值范围yoF1F2x代入椭圆方程:解:将xuy125)(14422xux22169288144144250xuxu22(288)4169(14414425)0uu由1313u1313yx22144169(25)0uu2169u例31、判断直线与椭圆位置关系的方法:解方程组消去其中一元得一元二次型方程△<0相离△=0相切△>0相交3、处理弦中点问题:“点差法”、“韦达定理”小结2122124)(1xxxxkAB2、弦长公式:),(),,(2211yxByxA已知2122124)(11yyyyk作业:•直线与椭圆相交于A、B,AB的中点坐标为.求直线的方程1422yx)21,1(ll作业:•1、如果椭圆的弦被(4,2)平分,求这弦所在的直线方程。193622yx练习:1、如果椭圆被的弦被(4,2)平分,那么这弦所在直线方程为()A、x-2y=0B、x+2y-4=0C、2x+3y-12=0D、x+2y-8=02、y=kx+1与椭圆恰有公共点,则m的范围()A、(0,1)B、(0,5)C、[1,5)∪(5,+∞)D、(1,+∞)3、过椭圆x2+2y2=4的左焦点作倾斜角为300的直线,则弦长|AB|=_______,DC193622yx1522myx1654.过椭圆221164xy内一点(2,1)M引一条弦,使弦被点M平分,求这条弦所在的直线方程.5.椭圆221164xy上的点到直线220xy最大距离是________.6.已知椭圆的焦点12(3,0),(3,0)FF且和直线90xy有公共点,则其中长轴最短的椭圆方程为______.240xy102214536xy