锐角三角函数VIP免费

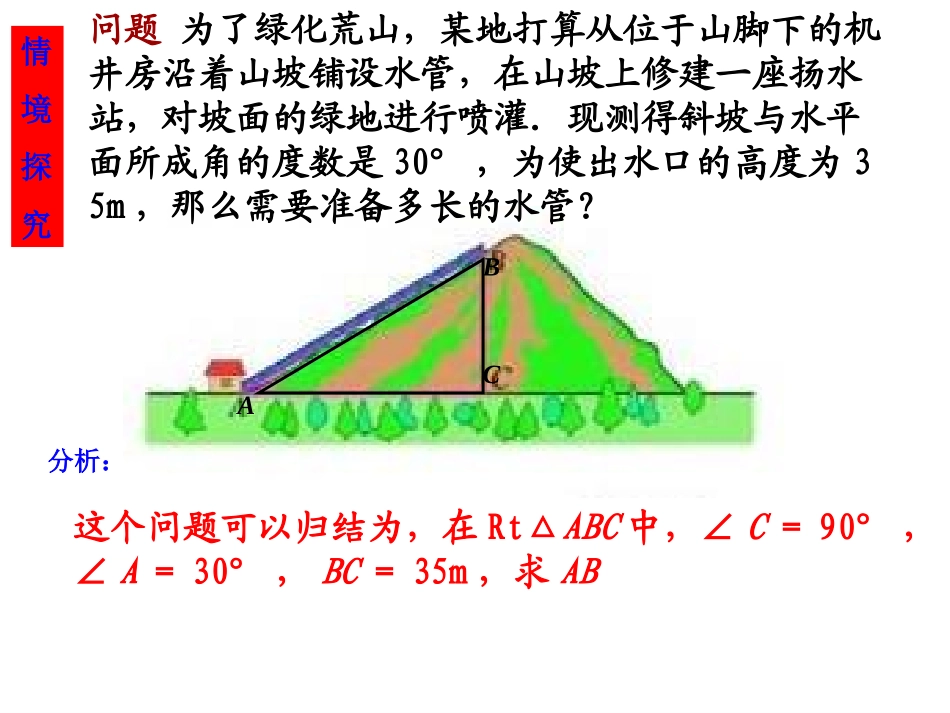
九年级数学(下册)第二十八章28.1锐角三角函数（1）怎么求塔身中心线偏离垂直中心线的角度比萨斜塔这个问题涉及到锐角三角函数的知识，学过本章之后，你就可以轻松地解答这个问题了！问题为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌．现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为35m，那么需要准备多长的水管？这个问题可以归结为，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝35m，求ABABC分析：情境探究在上面的问题中，如果使出水口的高度为50m，那么需要准备多长的水管？结论：在一个直角三角形中，如果一个锐角等于30°，那么不管三角形的大小如何，这个角的对边与斜边的比值都等于21ABC50m30mB'C'思考即在直角三角形中，当一个锐角等于45°时，不管这个直角三角形的大小如何，这个角的对边与斜边的比都等于22如图，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计算∠A的对边与斜边的比，你能得出什么结论？ABBCABC思考21综上可知，在一个Rt△ABC中，∠C＝90°，当∠A＝30°时，∠A的对边与斜边的比都等于，是一个固定值；当∠A＝45°时，∠A的对边与斜边的比都等于，也是一个固定值.22当∠A取其他一定度数的锐角时，它的对边与斜边的比是否也是一个固定值？这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比也是一个固定值．任意画Rt△ABC和Rt△A′B′C′，使得∠C＝∠C′＝90°，∠A＝∠A′＝α，那么与有什么关系．你能解释一下吗？ABBC''''BACB探究ABCA'B'C'如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦（sine），记作sinA即caAA斜边的对边sin例如，当∠A＝30°时，我们有2130sinsinA当∠A＝45°时，我们有2245sinsinA对边ABCcab斜边在图中∠A的对边记作a∠B的对边记作b∠C的对边记作c正弦函数例1如图，在Rt△ABC中，∠C＝90°，求sinA和sinB的值．例题示范ABC34求sinA就是要确定∠A的对边与斜边的比；求sinB就是要确定∠B的对边与斜边的比。解：在RtABC△中，因为AC=4、BC=3，所以AB=5，∴SinA=SinB=53ABBC54ABAC例2.如图,在Rt△ABC中,∠C=90°,AB=13,BC=5求sinA和sinB的值.ABC513,135==sinABBCA解:在RtABC△中,,125-13-2222BCABAC.1312==sin∴ABACB练一练1.判断对错:A10m6mBC1)如图(1)sinA=（）(2)sinB=（）(3)sinA=0.6m（）(4)SinB=0.8（）ABBCBCAB√√××sinA是一个比值（注意比的顺序），无单位；2)如图，sinA=（）BCAB×练习•课本：第64页第1、2题122.sinA是∠A的函数.ABC∠A的对边┌斜边斜边∠A的对边sinA=Sin300=sin45°=22对于∠A的每一个值（0°＜A＜90°），sinA都有唯一确定的值与之对应。小结锐角A的正弦课外作业•课本第68页复习巩固第1题求正弦值，第2题第1问，•第69页第6题，•第84页第1题的第1问