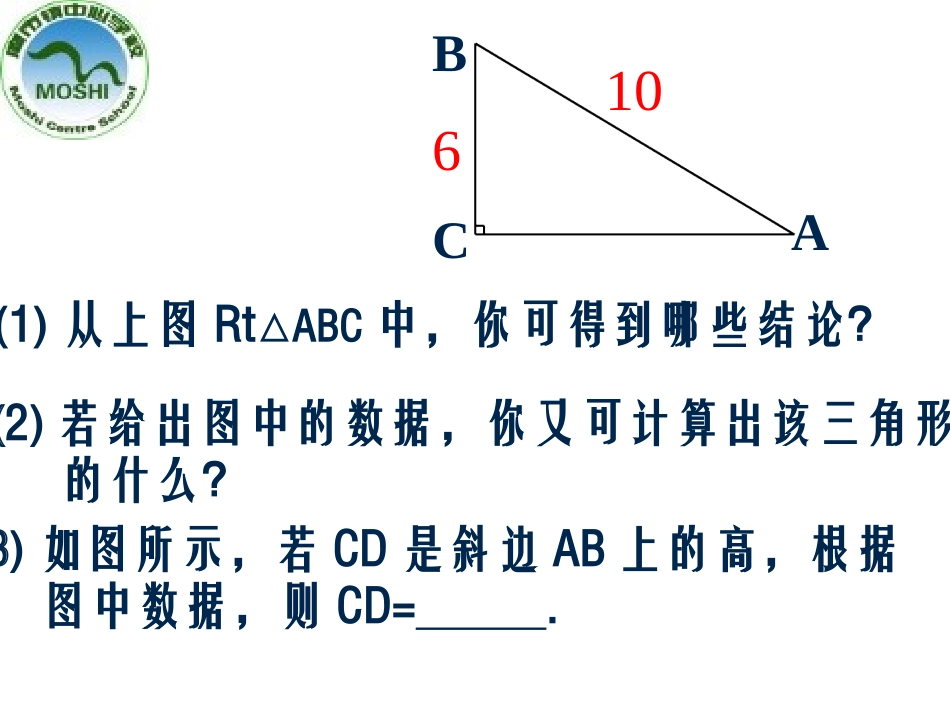
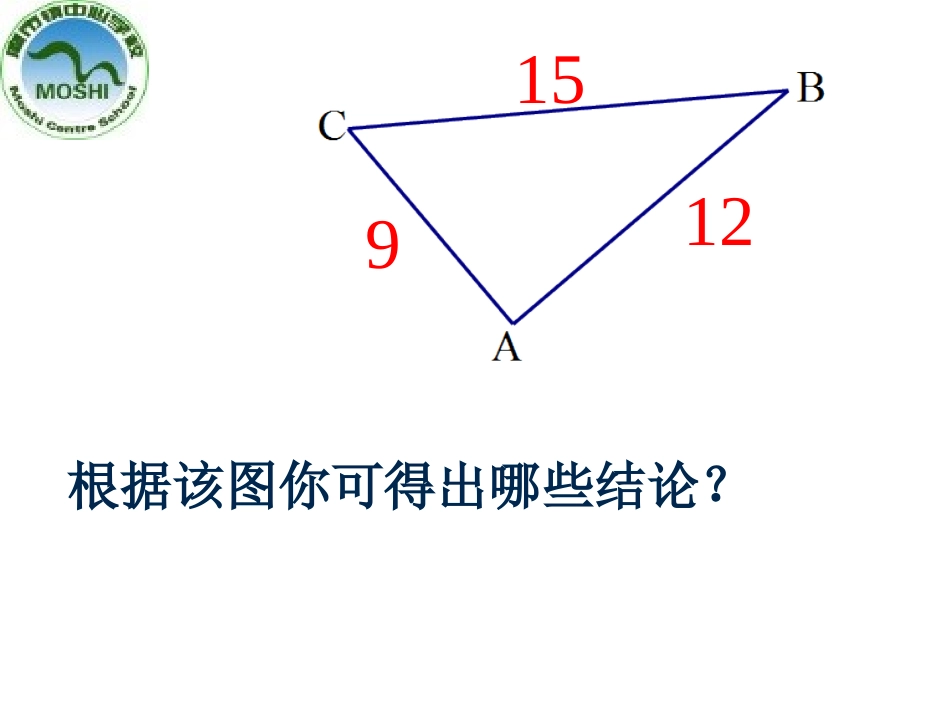
复习:第一章《勾股定理》执教者:朱院(1)从上图Rt△ABC中,你可得到哪些结论?(2)若给出图中的数据,你又可计算出该三角形的什么?CBA(3)如图所示,若CD是斜边AB上的高,根据图中数据,则CD=.10691215根据该图你可得出哪些结论?二、练习(一)、选择题1.已知一个Rt△的两边长分别为3和4,则第三边长的平方是()A、25B、14C、7D、7或252.下列各组数中,以a,b,c为边的三角形不是Rt△的是()A、a=1.5,b=2,c=3B、a=7,b=24,c=25C、a=6,b=8,c=10D、a=3,b=4,c=5DA3.若线段a,b,c组成Rt△,则它们的比为()A、234B∶∶、346∶∶C、51213∶∶D、467∶∶C1、在RtABC△中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若ab=34∶∶,c=10则SRtABC△=________。(二)、填空题2、直角三角形两直角边长分别为5和12,则它斜边上的高为__________。1320112413601.如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=8,AD=6,求AG的长.E(三)、解答题2.已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。3.如图,在长方体上有一只蚂蚁从项点A出发,要爬行到顶点B去找食物,一只长方体的长、宽、高分别为4、1、2,如果蚂蚁走的是最短路径,你能画出蚂蚁走的路线吗?C′′′总结:四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。4.如图,铁路上A,B两点相距25km,C,D为两村庄,DAAB⊥于A,CBAB⊥于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.(1)E站应建在离A站多少km处?(2)求两村与土特产品收购站围成的三角形的面积.5.已知,如图,在RtABC△中,∠C=90°,∠1=2∠,CD=1.5,BD=2.5,求AC的长.DACB12提示:作辅助线DEAB⊥,利用平分线的性质和勾股定理。解:过D点做DEAB⊥DACB12E∵∠1=2,C=90°∠∠∴DE=CD=1.5在RtDEB△中,根据勾股定理,得BE2=BD2-DE2=2.52-1.52=4BE=2∴在RtACD△和RtAED△中,∵CD=DE,AD=AD∴RtACDRtAED△△∴AC=AE令AC=x,则AB=x+2在RtABC△中,根据勾股定理,得AC2+BC2=AB2即:x2+42=(x+2)2x=3∴x三、小结本节课主要是应用勾股定理和它的逆定理来解决本节课主要是应用勾股定理和它的逆定理来解决实际问题,在应用定理时,应注意:实际问题,在应用定理时,应注意:1.1.没有图的要按题意画好图并标上字母;没有图的要按题意画好图并标上字母;2.2.不要用错定理;不要用错定理;3.3.求有关线段长问题,通常要引入未知数,求有关线段长问题,通常要引入未知数,根据有关的定理建立方程根据有关的定理建立方程,从而解决问题,从而解决问题;;4.空间问题要通过它的展开图转化为平面图形来解决四、作业教材P38:1,2,3,56.如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12,求这个三角形的面积.DABC如图,在△ABC中,AB=AC,P为BC上任意一点,求证:AB2-AP2=PB.PC。ABPC解:过A点做ADBC⊥ABPCD