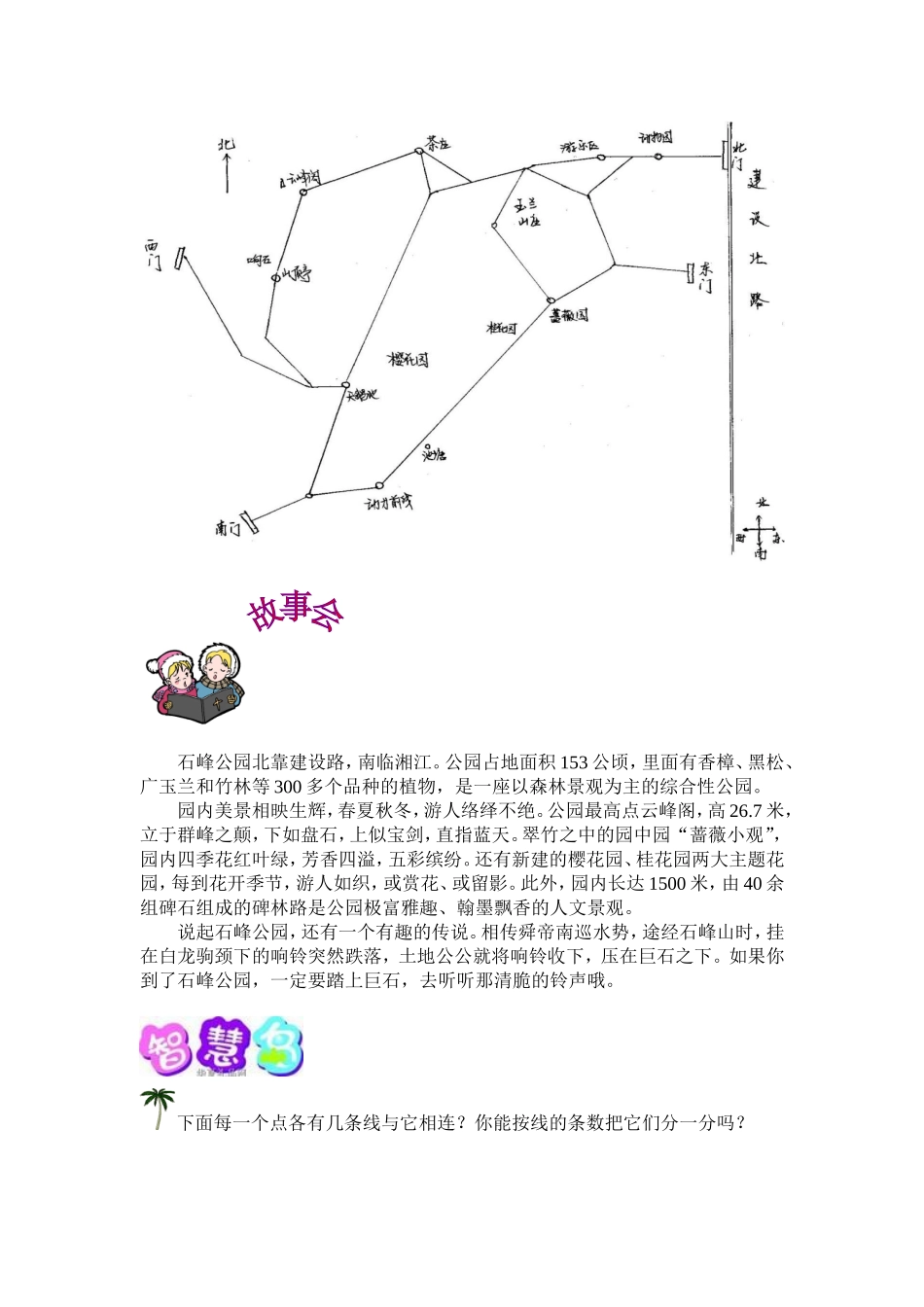
走进石峰公园(五年级上册)九方小学吴利军同学们,你们去过图片上的这些地方吗?知道这是哪里吗?对了,就是我们株洲美丽的“绿色明珠”——石峰公园。小明在游玩石峰公园时,想到了这样一个问题:有没有一条既可以参观公园的每个景点又可以不重复走的游玩路线?你能在下面的图上画一画,试着帮他找找吗?这就是有趣的一笔画问题,今天我们一起来探讨探讨吧。石峰公园北靠建设路,南临湘江。公园占地面积153公顷,里面有香樟、黑松、广玉兰和竹林等300多个品种的植物,是一座以森林景观为主的综合性公园。园内美景相映生辉,春夏秋冬,游人络绎不绝。公园最高点云峰阁,高26.7米,立于群峰之颠,下如盘石,上似宝剑,直指蓝天。翠竹之中的园中园“蔷薇小观”,园内四季花红叶绿,芳香四溢,五彩缤纷。还有新建的樱花园、桂花园两大主题花园,每到花开季节,游人如织,或赏花、或留影。此外,园内长达1500米,由40余组碑石组成的碑林路是公园极富雅趣、翰墨飘香的人文景观。说起石峰公园,还有一个有趣的传说。相传舜帝南巡水势,途经石峰山时,挂在白龙驹颈下的响铃突然跌落,土地公公就将响铃收下,压在巨石之下。如果你到了石峰公园,一定要踏上巨石,去听听那清脆的铃声哦。下面每一个点各有几条线与它相连?你能按线的条数把它们分一分吗?……我们把与奇数条线相连的点称作奇点。与偶数条线相连的点称为偶点。找出下面图形中的奇点个数和偶点个数,并填写下表。(1)(2)(3)(4)(5)(6)(7)(8)奇点个数偶点个数能否一笔画成图1图2图3图4图5图6图7图8观察表格,你有什么发现?和同学讨论讨论。下面的图形能一笔画出吗?为什么?(1)(2)欧拉定理:一个连通的图,并且奇点的个数等于0或2,那么它可以一笔画出;否则它不可以一笔画出。1、想一想,画一画,下面各图能一笔画成吗?2、现在你能不能用所学知识分析石峰公园有没有一条既可以参观的每个景点又可以不重复走的游玩路线?如果你是设计师,你会怎么增铺道路满足小明的这个要求。歌尼斯堡七桥问题18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡,那里有七座桥。如图1所示:河中的小岛A与河的左岸B、右岸C各有两座桥相连结,河中两支流间的陆地D与A、B、C各有一座桥相连结。哥尼斯堡的居民中流传着一道难题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点?这就是闻名的“哥尼斯堡七桥问题”。每一个到此游玩的人都想试一试,可是,对于这一看似简单的问题,却没有一个人能符合要求地从七座桥上走一遍。直到1836年,瑞士著名的数学家欧拉才证明了这个问题的不可能性。他把具体七桥布局化归为图2所示的简单图形,于是,七桥问题就变成一个一笔画问题:怎样才能从A、B、C、D中的某一点出发,一笔画出这个简单图形(即笔不离开纸,而且a、b、c、d、e、f、g各条线只画一次不准重复),并且最后返回起点?欧拉经过研究得出的结论是:图2是不能一笔画出的图形。这就是说,七桥问题是无解的。同学们,你们能不能利用今天所学的知识分析一下这个结论是如何产生的?图1图2欧拉(公元1707-1783年)出生在瑞士巴塞尔。小时候他就特别喜欢数学,不满10岁就开始自学《代数学》。小欧拉津津有味地读这本书,遇到不懂的地方,就用笔作个记号,事后再向别人请教。13岁时欧拉靠自己的努力考入了巴塞尔大学。这在当时是个奇迹,轰动了数学界。欧拉有着渊博的知识,无穷无尽的创作精力和空前丰富的著作,即使双目失明这样的灾祸降临,他也没有停止研究工作。欧拉具有惊人的心算才能,写出了几百篇非常优秀的论文。几乎每一个数学领域都可以看到欧拉的名字,他被誉为“现代数学之父”。