第二章整式乘法复习（）VIP免费

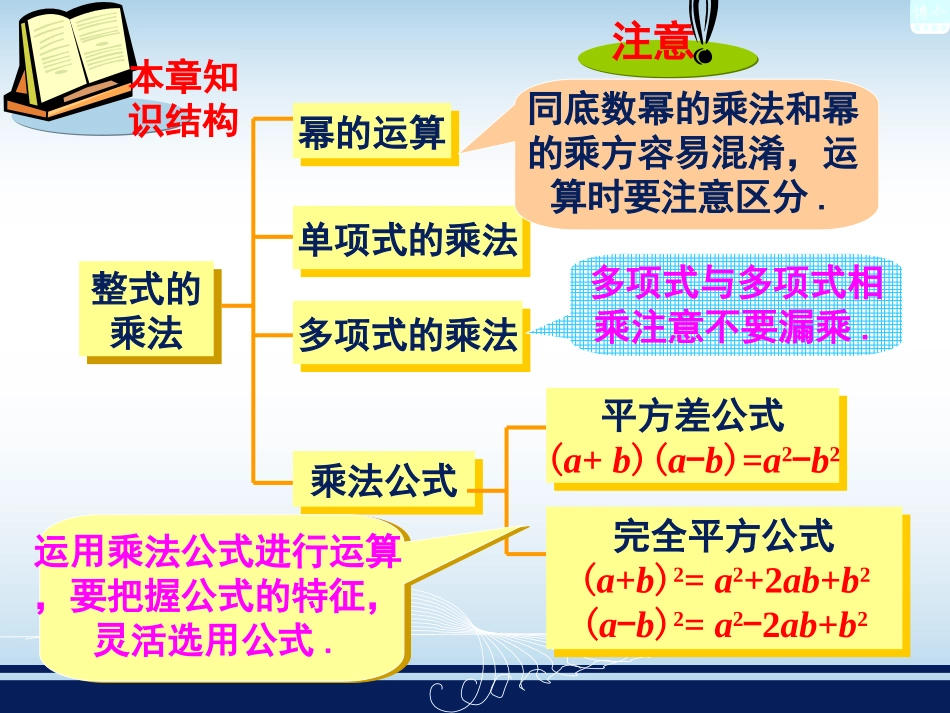
湘教版数学七年级（下）本节内容本章知识结构整式的乘法整式的乘法幂的运算幂的运算单项式的乘法单项式的乘法多项式的乘法多项式的乘法乘法公式乘法公式平方差公式(a+b)(a-b)=a2-b2平方差公式(a+b)(a-b)=a2-b2完全平方公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2完全平方公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2注意同底数幂的乘法和幂的乘方容易混淆，运算时要注意区分.多项式与多项式相乘注意不要漏乘.运用乘法公式进行运算，要把握公式的特征，灵活选用公式.整式的乘法同底数幂的乘法幂的乘方aman·=am+namn()=amn底数不变指数相乘指数相加mnnmaa)(nmnmaaa同底数幂相乘幂的乘方其中m,n都是正整数整式的乘法同底数幂的乘法幂的乘方积的乘方单项式的乘法aman·=am+namn()=amnabn()=anbna2x54·x2a3b(-3)=[4(-3)]a3a2()x2x5()b=-12a5bx7整式的乘法同底数幂的乘法幂的乘方积的乘方单项式的乘法单项式与多项式相乘多项式的乘法aman·=am+nam()n=amnabn()=anbna2x54·x2a3b(-3)m(a+b)=(a+b)(m+n)=ma+mbam+an+bm+bn想一想a2a3a5+=(1)a2aa2·=(2)(x-y)2(y-x)5=(x-y)7(8)x2()3=x5(4)a3x635-(x-y)7(y-x)7··47(6)(-5)(-5)=511-511(-3)2·33=(-3)5(7)2(5)35a·2a=10a610a5(3)a3a3=2a3a6公式的反向使用公式的反向使用nmnmaaamnnmmnaaabababa323210102101710410）（）（，求下列各式的值＝，＝已知公式的反向使用公式的反向使用试用简便方法计算试用简便方法计算::((abab))nn==aann··bbnn（（mm,,nn都是正整数都是正整数））反向使用反向使用::aann··bbnn==((abab))nn(1)(1)2233××5533;;(2)(2)((-5)5)1616××((-2)2)1515(3)(3)2244××4444××((-0.125)0.125)44;;=(2=(2××5)5)33=10=1033=(=(-5)5)××[([(-5)5)××((-2)]2)]1515==-55××10101515=[2=[2××44××((-0.125)]0.125)]44=1=144=1=1乘法公式平方差公式完全平方公式(a+b)(a-b)=a2b2-(a+b)2=a2b22ab++二次三项型乘法公式(x+a)(x+b)=x+(a+b)x+ab2例1计算1998200219982002=（2000-2）（2000+2）2222000=4000000-4=3999996解222222222)(______))(4(_____)()3(25___4___)2)(2(___6___))(1(yxyxbabaxxaaa：填空39520x2ab4xy口答练习二a2b2+-ab+=(a+b)2(1)a2b2+-ab+=(a-b)2(2)2(a+b)-(a-b)2=(3)2(a+b)+(a-b)2=(4)a2b2+=(a+b)2+(a-b)2+=(5)3ab（-ab）4ab2a22b2+（-2ab）2ab（3）如果a+a1=3,则a2+a21=()(A)7(B)9(C)10(D)11所以=9a+a1()2所以a+a1=922+2A故aa1=72+2因为a+a1=3解：分别为（）(4)若2a2-2ab+b2-2a+1=0,则a、b（A）1，-1（B）1，1（C）-1，1（D）0，0B(a-b)+(a-1)=022(a-b)=02(a-1)=02且所以a=1,b=1+22a-2abb-2a+1=02a+所以2+22a-2abb-2a+1=0因为解：(a-2b+3)(a+2b-3)的结果是（）（A）22a+4b+12b-9（C）22a+4b-12b-9（B）a2-4b2-12b-9（D）a2-4b2+12b-9D（5）计算=[a-(2b-3)][a+(2b-3)]=a2-(2b-3)2=a2-(4b-12b+9)2=a2-4b2+12b-9(a-2b+3)(a+2b-3)解：小结同底数幂的乘法幂的乘方积的乘方aman·=amn()=abn()=am+namnanbn平方差公式完全平方公式(a+b)(a-b)=a2b2-(a+b)2=a2b22ab++二次三项型乘法公式(x+a)(x+b)=x+(a+b)x+ab2