函数的最大（小）值与导数VIP免费

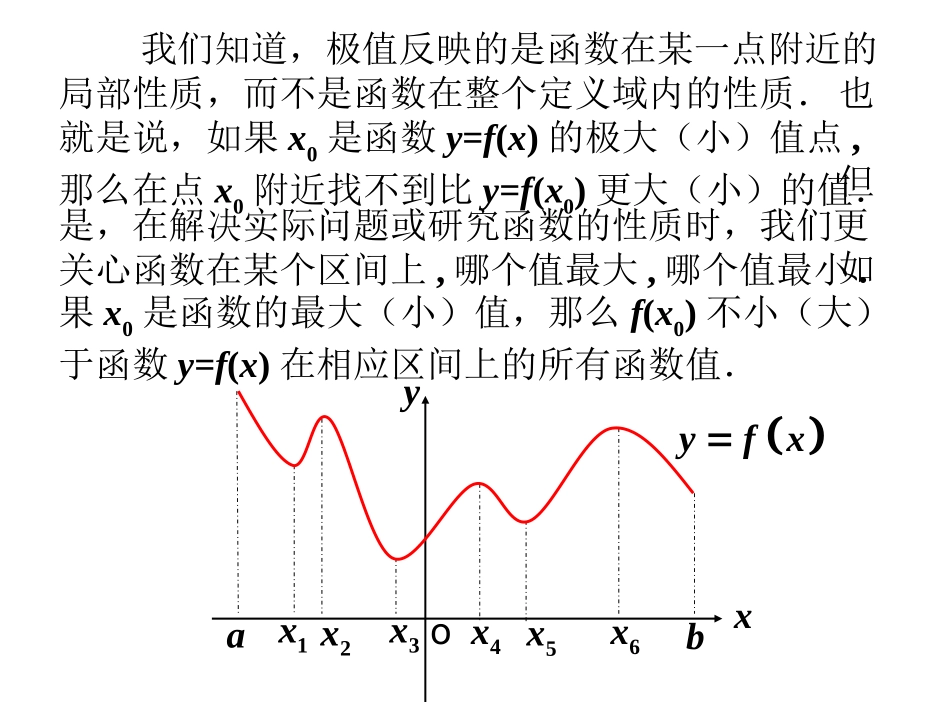
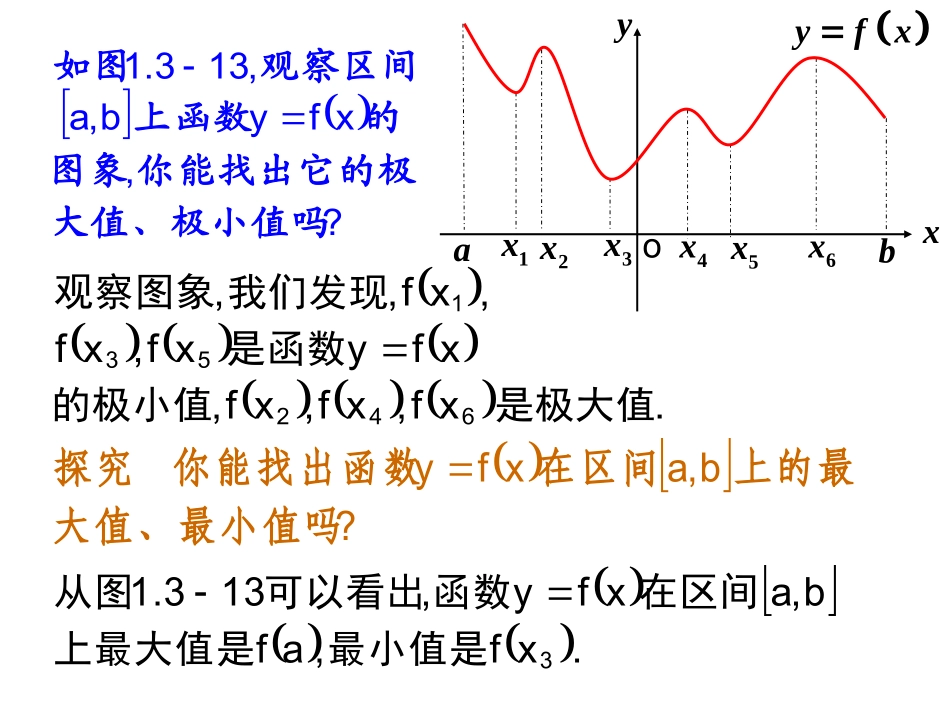
133..函数的最大小值与导数(1)我们知道，极值反映的是函数在某一点附近的局部性质，而不是函数在整个定义域内的性质．也就是说，如果x0是函数y=f(x)的极大（小）值点,那么在点x0附近找不到比y=f(x0)更大（小）的值．但是，在解决实际问题或研究函数的性质时，我们更关心函数在某个区间上,哪个值最大,哪个值最小.如果x0是函数的最大（小）值，那么f(x0)不小（大）于函数y=f(x)在相应区间上的所有函数值．a1x2x3xo4x5x6xbxyyfx?,xfyb,a,133.1大值、极小值吗你能找出它的极图象的上函数观察区间如图.xf,xf,xf,xfyxf,xf,xf,,642531是极大值的极小值是函数我们发现观察图象.xf,afb,axfy,133.13最小值是上最大值是在区间函数可以看出从图?b,axfy大值、最小值吗上的最在区间你能找出函数探究a1x2x3xo4x5x6xbxyyfxa1x2x3xo4x5xbxyxfy143.1图xfyabxyo153.1图?,?b,a,xfyb,a,153.1143.1么什最大值和最小值分别是如果有小值吗上有最大值、最它们在的图象上的函数观察中、在图a1x2x3xo4x5xbxyxfy143.1图xfyabxyo153.1图,,,.abyfx一般地如果在区间上函数的图象是一条连续不断的曲线那么它必有最大值和最小值a1x2x3xo4x5xbxyxfy143.1图xfyabxyo153.1图1.3141.315,,,,.yfx结合图、图以及函数极值中的例子不难看出只要把函数的所有极值连同端点的函数值进行比较就可以求出函数的最大值与最小值说明：1.在闭区间[a,b]上连续的函数必有最大值和最小值.这里有两层意思：（1）给定函数的区间必须是闭区间，f(x)在开区间上虽然连续但不能保证有最大值或最小值；（2）在闭区间上的每一点必须连续，即在闭区间上有间断点也不能保证f(x)有最大值和最小值.);1(0),10()(xxxxf（1）).1,0(,1)(xxxg（2）3.如果函数f(x)在[a,b]上连续，在(a,b)内可导，那么如何求f(x)在[a,b]内的最大值与最小值呢？①求函数f(x)在（a,b）内的极值；求f(x)在[a,b]上的最大值与最小值的步骤:②求函数f(x)在区间端点f(a),f(b)的值；③将函数f(x)在各极值与f(a),f(b)比较，其中最大的一个是最大值，最小的一个是最小值．2.极值与最值.注意区分函数的极值和函数的最值的联系与区别.函数的极值是函数的局部性质，函数的最值是函数在指定区间上的整体性质.解：)2)(2(42xxxy当x变化时，的变化情况如下表：yy,＋0－（2，3）2（0，2）yxy03342x令，解得0y311440,3.3fxxx例求函数在上的最大值与最小值41由表可知，函数在[0,3]上的最大值是4，最小值是．34oxy2331443fxxx163.1图0,3(1.316).fx上述结论可从函数在上的图象图得到直观验证解：xxy443,0y令则有0443xx解得.1,0,1x当x变化时，y’,y的变化情况如下表：1345413+0—0+0—2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2yx'y由表可知，函数在[-2,2]上的最大值是13，最小值是4．练习1求函数在[-2,2]上的最大值与最小值．5224xxy4(1)(1)xxx①求函数f(x)在（a,b）内的极值；求函数y=f(x)在[a,b]上的最大值与最小值的步骤:②求函数f(x)在区间端点f(a),f(b)的值；③将函数f(x)在各极值与f(a),f(b)比较，其中最大的一个是最大值，最小的一个是最小值．例2.设f(x)=ax3+bx+c(a≠0)为奇函数,其图象在(1,f(1))处切线与直线x-6y-7=0垂直,导函数f’(x)最小值为-12．（Ⅰ）求a，b，c的值；（Ⅱ）求函数f(x)的单调递增区间，并求函数f(x)在[-1,3]上的最大值和最小值．解：（Ⅰ） f(x)为奇函数，)()(xfxf即cbxaxcbxax33.0c)('xf又bax23.12b 直线x-6y-7=0的斜率为,61,63)1('baf.2a.0,12,2cba的最小值为-12（Ⅱ）xxxf122)(3126)('2xxf)2)(2(6xxx)(xf)('xf列表如下：0)('xf令得，.2,221xx)2,(2)2,2(2),2(＋－＋00极大值极小值∴函数的单调增区间是,)2,(.),2()1(f,10)2(f,28,18)3(f,18∴函...