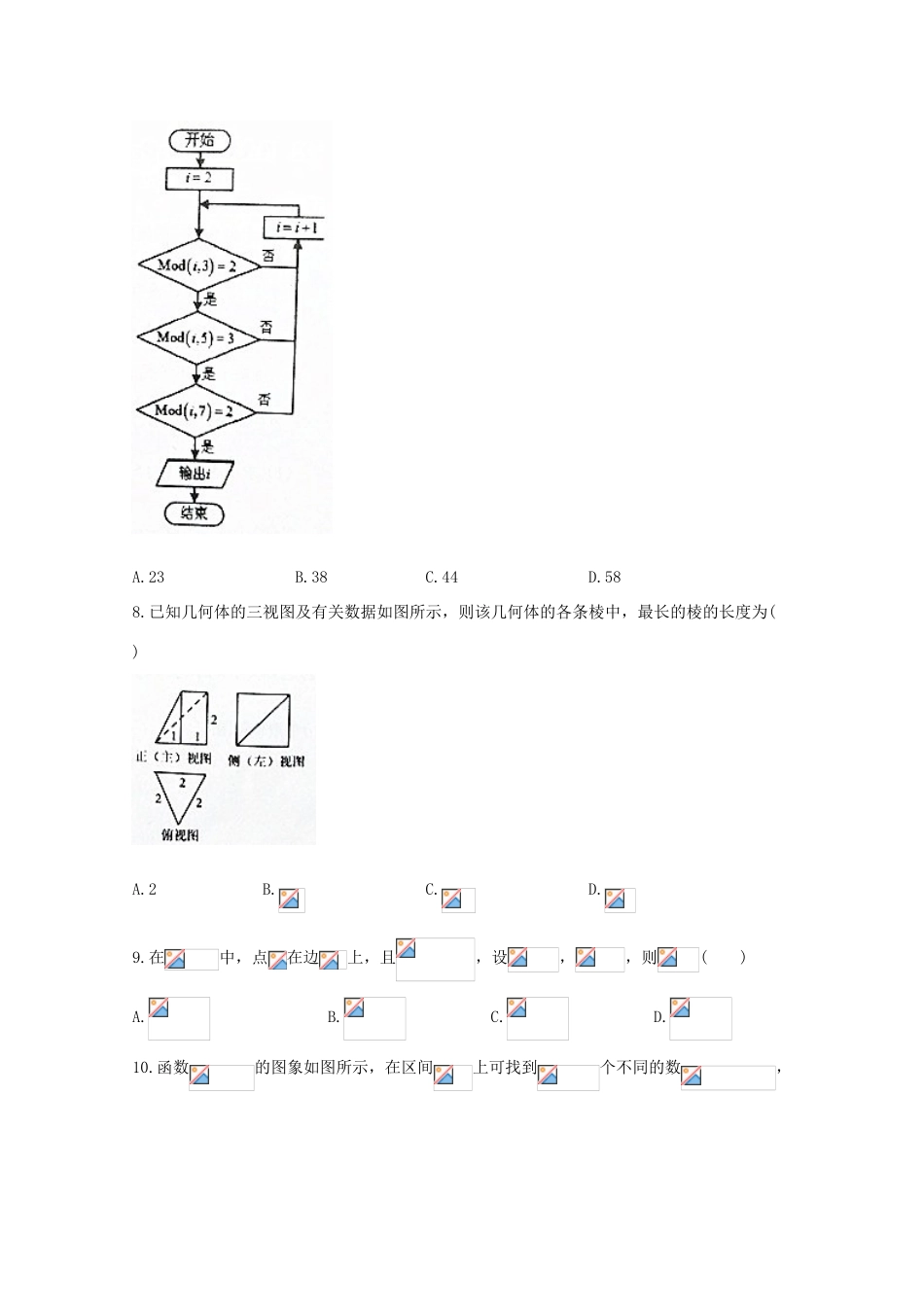
河南省南阳市第一中学2018届高三数学第九次考试试题文一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则()A.B.C.D.2.已知(为虚数单位),且,则()A.B.C.D.23.已知命题,,则是成立的()条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要4.已知某厂的产品合格率为,现抽出10件产品检查,则下列说法正确的是()A.合格产品少于8件B.合格产品多于8件C.合格产品正好是8件D.合格产品可能是8件5.()A.B.C.D.6.等差数列的前项和,,,则的值为()A.40B.52C.56D.647.如图的程序框图的算法思路源于我国古代著名的“孙子剩余定理”,图中的表示正整数除以正整数后的余数为,例如.执行该程序框图,则输出的等于()A.23B.38C.44D.588.已知几何体的三视图及有关数据如图所示,则该几何体的各条棱中,最长的棱的长度为()A.2B.C.D.9.在中,点在边上,且,设,,则()A.B.C.D.10.函数的图象如图所示,在区间上可找到个不同的数,使得,则的取值范围是()A.B.C.D.11.设奇函数在内有9个零点,则的取值范围为()A.B.C.D.12.已知抛物线的准线与轴交于点,焦点是,是抛物线上任意一点,当取得最小值时,点恰好在以为焦点的双曲线上,则该双曲线的离心率为()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.抛物线的准线方程是______________.14.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为______________.15.平面过正方体的顶点,平面,平面,平面,则所成角的大小为______________.16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料,乙材料.用5个工时;生产一件产品B需要甲材料,乙材料,用3个工时。生产一件产品A的利润为2100元,生产一件产品B的利润为900元,该企业现有甲材料150,乙材料,则在不超过600个工时的条件下,生产产品A,产品B的利润之和的最大值为______________元.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列是各项均为正数的等比数列,若,.(1)设,求数列的通项公式;(2)求数列的前项和.18.随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:用户编号评分用户编号评分用户编号评分用户编号评分1781188217931932731286228332783811395237233754921476247434815951597259135846851678266636777791788278037818841882288338769631976297439851086208930824089用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.(1)请你列出抽到的10个样本的评分数据;(2)计算所抽到的10个样本的均值和方差;(3)在(2)的条件下,若用户的深意度评分在之间,则满意度等级为“级”,试应用样本估计总体的思想,估计该地区满意度等级为“级”的用户所占的百分比是多少?(精确到)19.在四棱锥中,,平面平面,.,是上一点.(1)证明:平面平面;(2)若是正三角形,且是中点,求三棱锥的体积.20.已知椭圆的离心率为,左、右焦点分别为、,过的直线交椭圆于两点.(1)若以为直径的圆内切于圆,求椭圆的长轴长;(2)当时,问在轴上是否存在定点,使得为定值?并说明理由.21.已知函数.(1)若,求函数的图像在点处的切线方程;(2)若函数有两个极值点,,且,求证:.22.在直角坐标系中,曲线(为参数,),在以为极点,轴正半轴为极轴的极坐标系中,直线.(1)若与曲线没有公共点,求的取值范围;(2)若曲线上存在点到距离的最大值为,求的值.23.设函数,.(1)求不等式的解集;(2)已知关于的不等式的解集为,若,求实数的取值范围.答案一、选择题1-5:CABDD6-10:DACBB11、12:AB二、填空题13.14.15.16.216000元三、解答题17.解:(1)由数列是各项均为正数的等比数列,且,∴,即:.又 ,∴.(2)由(1)可知,则①②①-②∴.18.解:(1)由题意得,通过系统抽样分别抽取编号为4,8,12,16,20,24,28,32,36,40的评分数据...