高三数学第九次模拟考试试题 文-人教版高三全册数学试题VIP免费

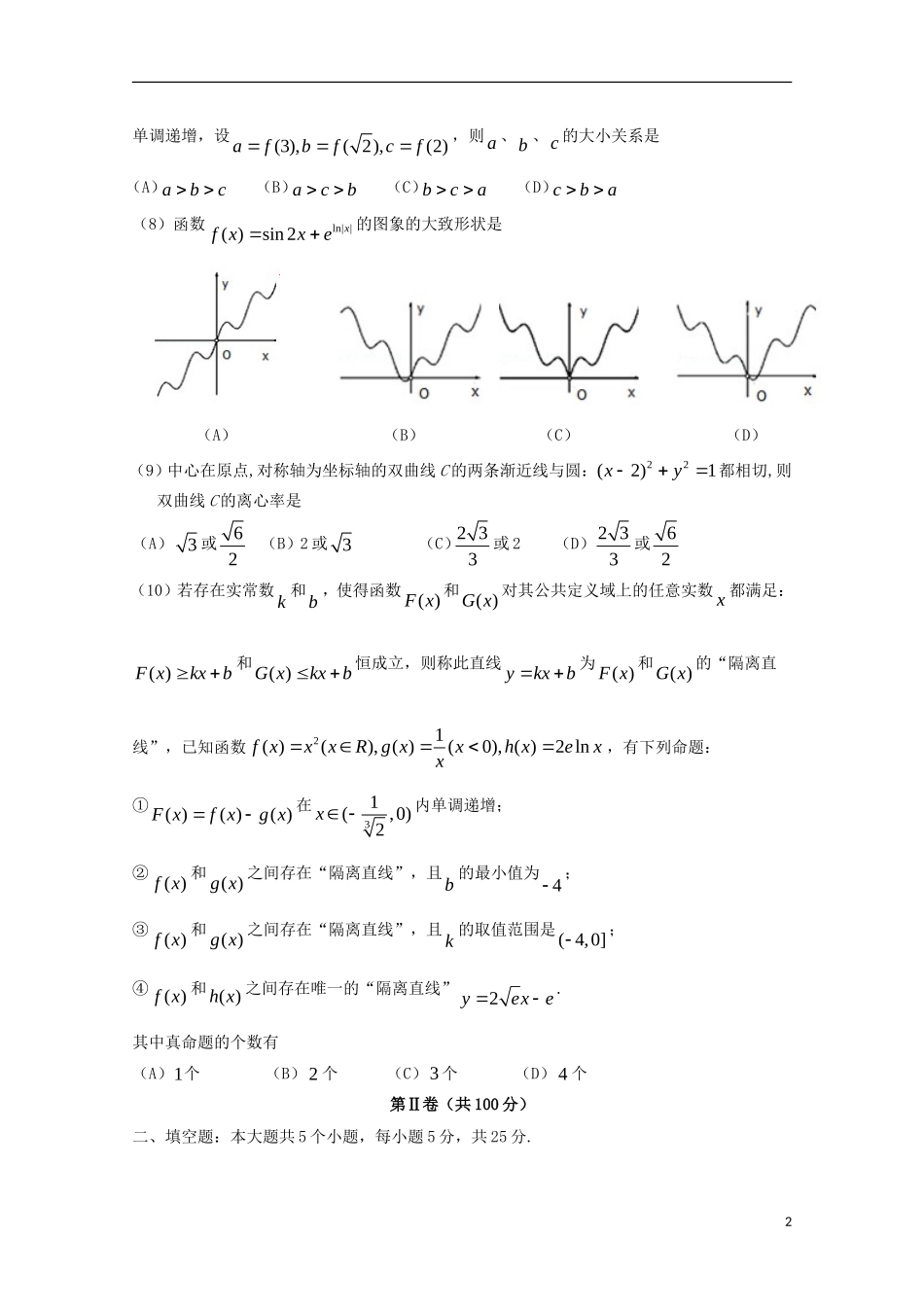
2012级高三第九次模拟考试试题第I卷（共50分）一、选择题：本大题共10个小题，每小题5分，共50分.每小题给出的四个选项中只有一项是符合题目要求的.（1）设集合{1,2,3,4},{1,2,3},{2,3,4}UMN，则)(NMCU=（A）{1,2}（B）{2,3}（C）{2,4}（D）{1,4}（2）复数4312ii的实部是（A）2（B）2（C）3（D）4（3）函数12log43yx的定义域为（A）3(,)4（B）3(,)4（C）3(,1]4（D）3(,1)4（4）下列有关命题的说法错误的是（A）命题“若210x，则1x”的逆否命题为：“若1x则210x”（B）“1x”是“2320xx”的充分不必要条件（C）若pq为假命题，则p、q均为假命题（D）对于命题R:xp使得210xx，则R:xp均有210xx…（5）若关于,xy的不等式组0010xxykxy，表示的平面区域是直角三角形区域，则正数k的值为（A）1（B）2（C）3（D）4（6）一个棱锥的三视图如图，则该棱锥的表面积为（A）48122（B）48242（C）72122（D）72242（7）定义在R上的函数()fx满足：(1)(1)(1)fxfxfx成立，且()fx在[1,0]上1单调递增，设(3),(2),(2)afbfcf，则a、b、c的大小关系是（A）abc（B）acb（C）bca（D）cba（8）函数||ln2sin)(xexxf的图象的大致形状是（A）（B）（C）（D）（9）中心在原点,对称轴为坐标轴的双曲线C的两条渐近线与圆：1)2(22yx都相切,则双曲线C的离心率是（A）3或62（B）2或3（C）233或2（D）233或62（10）若存在实常数k和b，使得函数()Fx和()Gx对其公共定义域上的任意实数x都满足：()Fxkxb和()Gxkxb恒成立，则称此直线ykxb为()Fx和()Gx的“隔离直线”，已知函数21()(),()(0),()2lnfxxxRgxxhxexx，有下列命题：①()()()Fxfxgx在31(,0)2x内单调递增；②()fx和()gx之间存在“隔离直线”，且b的最小值为4；③()fx和()gx之间存在“隔离直线”，且k的取值范围是(4,0]；④()fx和()hx之间存在唯一的“隔离直线”2yexe.其中真命题的个数有（A）1个（B）2个（C）3个（D）4个第Ⅱ卷（共100分）二、填空题：本大题共5个小题，每小题5分，共25分.2（11）已知定义在R上的函数()yfx的图象在点(1,(1))Mf处的切线方程为122yx，则(1)(1)ff_____.（12）在区间上随机取一个数x,则]2,1[cossinxx的概率是.（13）执行如图所示的程序框图，则输出的S的值是_____.（14）已知过点M(－3,0)的直线l被圆x2＋(y＋2)2＝25所截得的弦长为8，那么直线l的方程为________．（15）设函数()fx的定义域为D，如果存在正实数k，对于任意,xD都有xkD，且()()fxkfx恒成立，则称函数()fx为D上的“k型增函数”，已知函数()fx是定义在R上的奇函数，且当0x时，()2fxxaa，若()fx为R上的“2015型增函数”，则实数a的取值范围是______.三、解答题：本大题共6小题，共75分.（16）(本小题满分12分)已知函数27()sin22sin1()6fxxxxR，（Ⅰ）求函数fx的周期及单调递增区间；（Ⅱ）在ABC中，三内角A，B，C的对边分别为cba,,，已知函数fx的图象经过点1,,,,2Abac成等差数列，且9ABAC�，求a的值.（17）(本小题满分12分)在某高校自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为,,,,ABCDE五个等级.某考场考生的两科考试成绩数据统计如下图所示，其中“数学与逻辑”科目的成绩为B的考生有10人.（Ⅰ）求该考场考生中“阅读与表达”科目中成绩为A的人数；3第（17）题图（Ⅱ）若等级,,,,ABCDE分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分；（Ⅲ）已知参加本考场测试的考生中，恰有两人的两科成绩均为A.在至少一科成绩为A的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为A的概率.（18）(本小题满分12分)已知三棱柱ABC－CBA中，平面BCBC⊥底面ABC，BB′⊥AC，底面ABC是边长为2的等边三角形，AA＝3，E、F分别在棱AA，CC上，且AE＝FC＝2.（Ⅰ）求证：BB⊥底面ABC；（Ⅱ）在棱BA...