高三数学理轨迹、解析与向量人教版知识精讲VIP免费

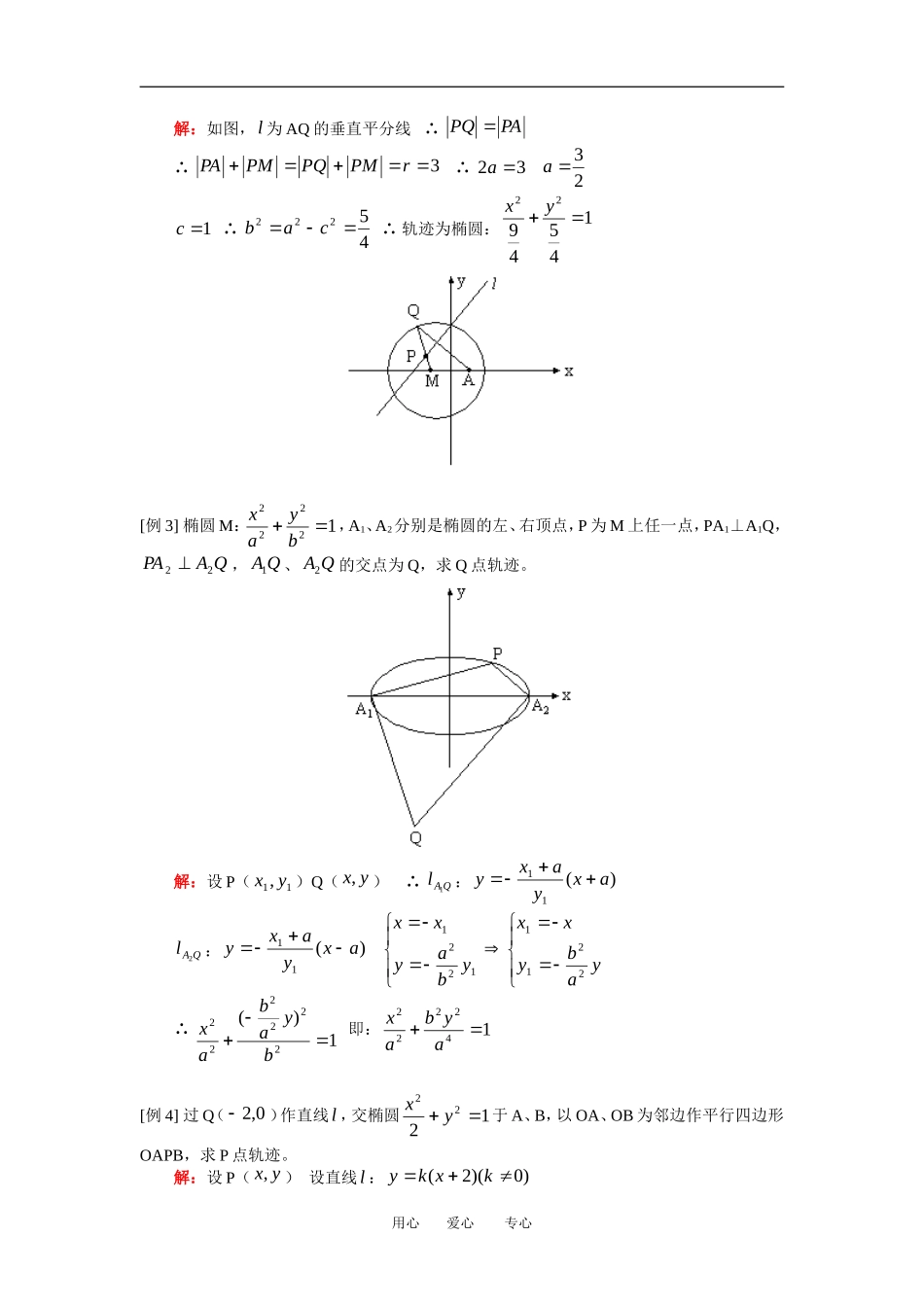
高三数学理轨迹、解析与向量人教版【同步教育信息】一.本周教学内容：轨迹、解析与向量二.重点、难点：（一）轨迹的求法1.直接法2.几何法3.转移法4.参数法（二）向量与解析依题意，用向量运算、定义、发现坐标及参数之间的关系，最后通常均转化为解析问题。【典型例题】[例1])0,2(),0,2(BA，动点M满足MABMBA2，求M的轨迹。解：设),(yxM（1）M在线段AB上，0MABMBA成立（2）M不在线段AB上，MABMBA∴图形在y轴右侧不妨设M在x轴上方①90MBA2tanxyMAB2tanxyMBAMABMBA2tantan2)2(1222xyxyxy∴044322xyx*②90MBA时，M（2，4）满足*式∴轨迹为0y（22x）或044322xyx（0x）[例2]圆M：9)1(22yx，A（1，0），Q在M上，线段AQ的垂直平分线交半径MQ于P，求P点轨迹。用心爱心专心解：如图，l为AQ的垂直平分线∴PAPQ∴3rPMPQPMPA∴32a23a1c∴45222cab∴轨迹为椭圆：1454922yx[例3]椭圆M：12222byax，A1、A2分别是椭圆的左、右顶点，P为M上任一点，PA1⊥A1Q，QAPA22，QA1、QA2的交点为Q，求Q点轨迹。解：设P（11,yx）Q（yx,）∴QAl1：)(11axyaxyQAl2：)(11axyaxy1221ybayxxyabyxx2211∴1)(222222byabax即：142222aybax[例4]过Q（0,2）作直线l，交椭圆1222yx于A、B，以OA、OB为邻边作平行四边形OAPB，求P点轨迹。解：设P（yx,）设直线l：)0)(2(kxky用心爱心专心12)2(22yxxky∴0)28(8)21(2222kxkxk0)28)(21(464224kkk∴)22,0()0,22(k设BABAyyyxxx00∴222214218kkykkxk为参数)22,0()0,22(k∴kyx2yxk2代入∴124)2(22yx02x半个椭圆[例5]已知A（0,2），B（2，0）点C，点D满足2AC，)(21ACABAD（1）求D点轨迹；（2）经点A作直线l交以A、B为焦点的椭圆于M、N两点。线段MN的中点到y轴的距离为54，且直线l与点D的轨迹相切，求椭圆方程。解：（1）设C（00,yx）D（yx,）∴),2(00yxAC，)0,4(AB 2AC∴4)2(2020yxABACAD2∴),6(),2(200yxyx∴002642yyxx∴yyxx22200代入44)222(22yx∴122yx（2）设椭圆方程为)4(1422222aayaxl：)2(xkyl与D的轨迹相切1122kk∴312k用心爱心专心0444)4(14)2(24222222222222aakaxkaxakaayaxxky即：0443)3(24222aaxaxa*54)3(222221aaxx82a代入检验*式0∴椭圆方程14822yx[例6]动点P与双曲线13222yx的两个焦点21,FF距离之和为定值，且21cosPFF的最小值为91。（1）求P点轨迹；（2）若已知点D（0，3），点M，N在P的轨迹上，且DNDM，求的取值范围。解：（1）设P的轨迹为椭圆12222byax5322cP在短轴顶点时，21PFF最大21cosPFF最小∴91220222aa∴92a∴14922yx（2）设M（11,yx）N（22,yx） DNDM∴)3,()3,(2211yxyx∴3)3(2121yyxx14]3)3([9)(14922222222yxyx消2x2222214)(4)33(yy)1)(1()]1(32[)1(432y用心爱心专心)1(3)1(3422y∴65132y 22y∴26513551[例7]无论m为何值，直线l：mxy与双曲线C：12222byx（0b）恒有公共点。（1）求C的离心率e的取值范围；（2）若直线l过C的右焦点F与双曲线交于P、Q，并且满足FQFP51，求C的方程。解：（1）02)2(21222222222bmmxxxbbyxmxy∴0)(24)2(2222bmmxxb①022b时，0m方程组无解不合题意②022b，0)2(224mbb恒成立即222mb恒成立∴22b222222bacace∴2e（2）设l：cxy，12222byxcxy∴022)2(222222bcbcybyb∴222221bcbyy22222...