高三数学理第一轮复 习：线性规化；圆的方程人教版VIP免费

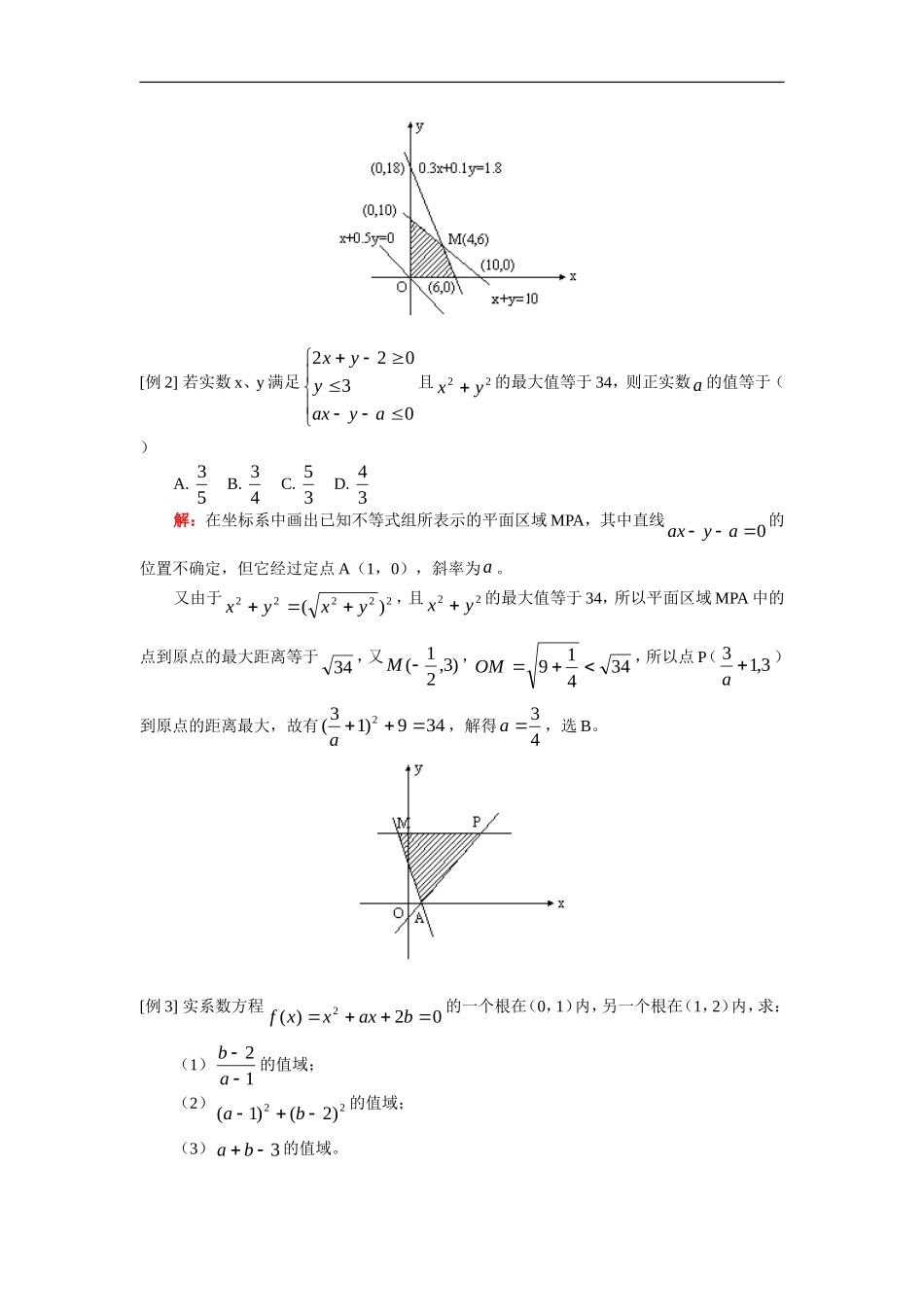
高三数学理第一轮复习：线性规化；圆的方程人教版【本讲教育信息】一.教学内容：线性规化；圆的方程二.本周教学重、难点：1.了解二元一次不等式表示平面区域；了解线性规划的意义，并会简单地应用。2.掌握圆的标准方程和一般方程，了解参数方程的概念（2006年理科考试大纲新增加），理解圆的参数方程。（2006年文科考试大纲新增加）。【典型例题】[例1]某投资人打算投资甲、乙两个项目，根据预测甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？解：设投资人分别用x万元，y万元投资甲、乙两个项目。由题意知008.11.03.010yxyxyx目标函数yxz5.0上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域。作直线0l：05.0yx，并作平行于直线0l的一组直线zyx5.0，Rz。与可行域相交，其中有一条直线经过可行域上的M点，且与直线05.0yx的距离最大，这里M点是直线10yx和8.11.03.0yx的交点。解方程组8.11.03.010yxyx得4x，6y此时765.041z（万元） 07∴当6,4yx时z取得最大值答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大。[例2]若实数x、y满足03022ayaxyyx且22yx的最大值等于34，则正实数a的值等于（）A.53B.43C.35D.34解：在坐标系中画出已知不等式组所表示的平面区域MPA，其中直线0ayax的位置不确定，但它经过定点A（1，0），斜率为a。又由于22222)(yxyx，且22yx的最大值等于34，所以平面区域MPA中的点到原点的最大距离等于34，又)3,21(M，34419OM，所以点P（3,13a）到原点的距离最大，故有349)13(2a，解得43a，选B。[例3]实系数方程02)(2baxxxf的一个根在（0，1）内，另一个根在（1，2）内，求：（1）12ab的值域；（2）22)2()1(ba的值域；（3）3ba的值域。解：由题意0201200)2(0)1(0)0(bababfff如图所示，A（1,3）、B（0,2）、C（0,1）又由所要求的量的几何意义知其值域分别为（1）（1,41）；（2）（8，17）；（3）（4,5）[例4]求圆心在直线xy4上，并且与直线l：01yx相切于点P（2,3）的圆的方程。解：设所求圆的方程为222)()(rbyax依题意有rbarbaab21)2()3(4222解得22,4,1rba∴所求圆的方程为8)4()1(22yx[例5]已知圆0622myxyx与直线032yx相交于P、Q两点，O为坐标原点，若OP⊥OQ，求实数m的值。解：设点P、Q的坐标分别为),)(,(2211yxyx，由OP⊥OQ，得02121yyxx①由0603222myxyxyx消去y并整理，得02741052mxx 5274,22121mxxxx②又 P、Q在直线032yx上∴)3(21)3(212121xxyy])(39[412121xxxx512m③将②③代入①有051252742121mmyyxx解得3m，适合0∴3m[例6]已知实数yx、满足方程01422xyx，求（1）xy的最大值和最小值；（2）xy的最小值；（3）22yx的最大值和最小值。解：（1）如图，方程01422xyx表示以点（2，0）为圆心，以3为半径的圆设kxy，即kxy当圆心（2，0）到kxy的距离为半径时直线与圆相切，斜率取得最大、最小值由31022kk，解得32k所以3,3minmaxkk（也可由平面几何知识，有60,3,2POCOPOC，直线OP的倾斜角为60，直线PO的倾斜角为120，解之，即得）（2）设bxy，则bxy，仅当直线bxy与圆切于第四象限时，纵轴截距b取最小值。由点到直线的距离公式，得3202b，即62b故62)(minxy（3）22yx是圆上点与原点距离之平方，故连结OC，与圆交于B点，并延长交圆于C，则347)32()(22max22COyx，347)32()(22min22...