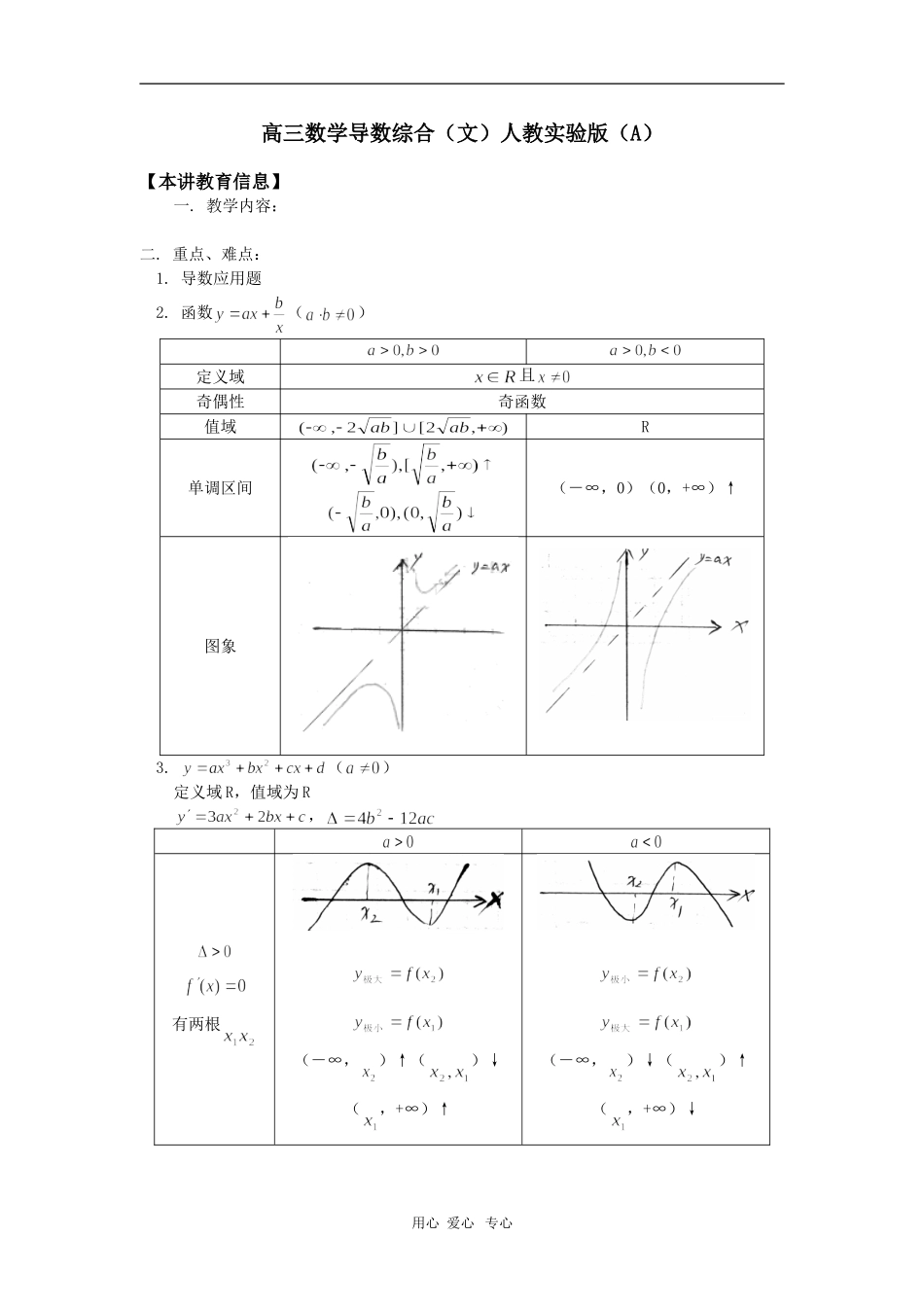
高三数学导数综合(文)人教实验版(A)【本讲教育信息】一.教学内容:二.重点、难点:1.导数应用题2.函数()定义域且奇偶性奇函数值域R单调区间(-∞,0)(0,+∞)↑图象3.()定义域R,值域为R,有两根(-∞,)↑()↓(,+∞)↑(-∞,)↓()↑(,+∞)↓用心爱心专心R上↑无极值R上↓无极值【典型试题】[例1]研究函数的性质。解:∴(-∞,-1)↓(-1,1)↑(1,+∞)↓定义域R,值域奇函数[例2]已知二次函数的图像过原点和点(m,0)与点(m+1,m+1)(I)求的表达式;(II)设且在和()处取到极值。(1)求证:;(2)若,则过原点且与曲线相切的两条直线能否互相垂直?若能,则给出证明;若不能,请说明理由?解:(I)设(),由题意得,解得∴(II) ∴①由题意知,为方程的两个实根用心爱心专心又,,∴两根分布在(0,n)(n,m)内又∴②设两切点的横坐标分别为,则切线的方程为又过原点,∴解得或,同理或,∴[例3]已知函数在x=0处取得极值,曲线过原点和点P(-1,2),若曲线在点P处的切线与直线的夹角为45°,且该切线的倾斜角为钝角。(1)求的表达式;(2)求的单调区间。解:(1) 曲线过原点∴∴,又是的极值点∴∴(2分)又 过点P(-1,2)的切线斜率为,又由题意解得:(不合题意,舍去)由即解得∴(2),令得或所以在区间(-∞,-2)和(0,+∞)在内为增函数令得,所以在区间(-2,0)内为减函数综上知的单调区间为(-∞,-2),(0,+∞),(-2,0)[例4]已知函数,当时,取得极大值7;当x=3时,取得极小值。(1)求的值及函数的极小值;(2)若对任意,不等式恒成立,试确定实数的最小用心爱心专心值。(1)解:, 及x=3时取得极值∴-1,3是方程的根,即为的两根由一元二次方程根与系数的关系,有∴∴ 时极大值是7,∴,极小值∴极小值为-25(2)解:由(1)知在(-1,0)上是减函数且在[-1,0]上最大值,在[-1,0]上最小值对任意(-1,0)恒有成立∴,即的最小值为5[例5]已知函数,其中。(1)求证:函数取极大值和极小值的点各有一个;(2)当的极大值为1,极小值为-1时,过曲线上一点P(3,)作这条曲线的切线,求此切线的方程。(1)证明:令,即(*) ,故方程(*)有两个不等的实根,记为,不妨设,,的变化情况如下表:(-∞,)(,)(,+∞)-0+0-↓极小值↑极大值↓由表可见,取极大值和极小值的点各有一个用心爱心专心(2)解:由(1),可知即两式相加,得③又,代入③,得∴而∴∴,代入(*),得 ∴,代入①,得∴函数解析式为当x=3时,,∴P(3,)又,由点斜式知所求切线方程为[例6]已知函数(1)若在上是单调减函数,求实数的取值范围;(2)设,若不等式对一切恒成立,求实数的取值范围。(1)令在上是减函数由,得∴在上是增函数,对<0恒成立又 ∴恒成立,即 ,故,可得,∴综上可得(2)用心爱心专心=令, ,则,令当时,显然不成立当时,当且仅当时,取最小值①当时,在为减函数且恒成立解,得②当,则,即不成立综上得[例7]已知在时取得极值,且。(1)试求常数的值;(2)试判断是函数的极小值还是极大值,并说明理由。解:(1) 是函数的极值点,∴是方程,即的两根由根与系数的关系,得又∴③由①②③解得(2),∴当或时,,当时,∴函数在(-∞,-1)和(1,+∞)上是增函数,在(-1,1)上是减函数∴当x=-1时,函数取得极大值,当x=1时,函数取得极小值用心爱心专心[例8]已知,且(1)设,求的解析式;(2)设,试问:是否存在实数,使在(-∞,-1)内为减函数,且在(-1,0)内是增函数。解:(1)由题意得 ∴,∴,∴(2)若满足条件的存在,则 函数在(-∞,-1)上是减函数,∴当时,即对于(-∞,-1)恒成立∴ ,∴,∴,解得又函数在(-1,0)上是增函数,∴当-1