高三数学导数专题 新课标 人教版VIP免费

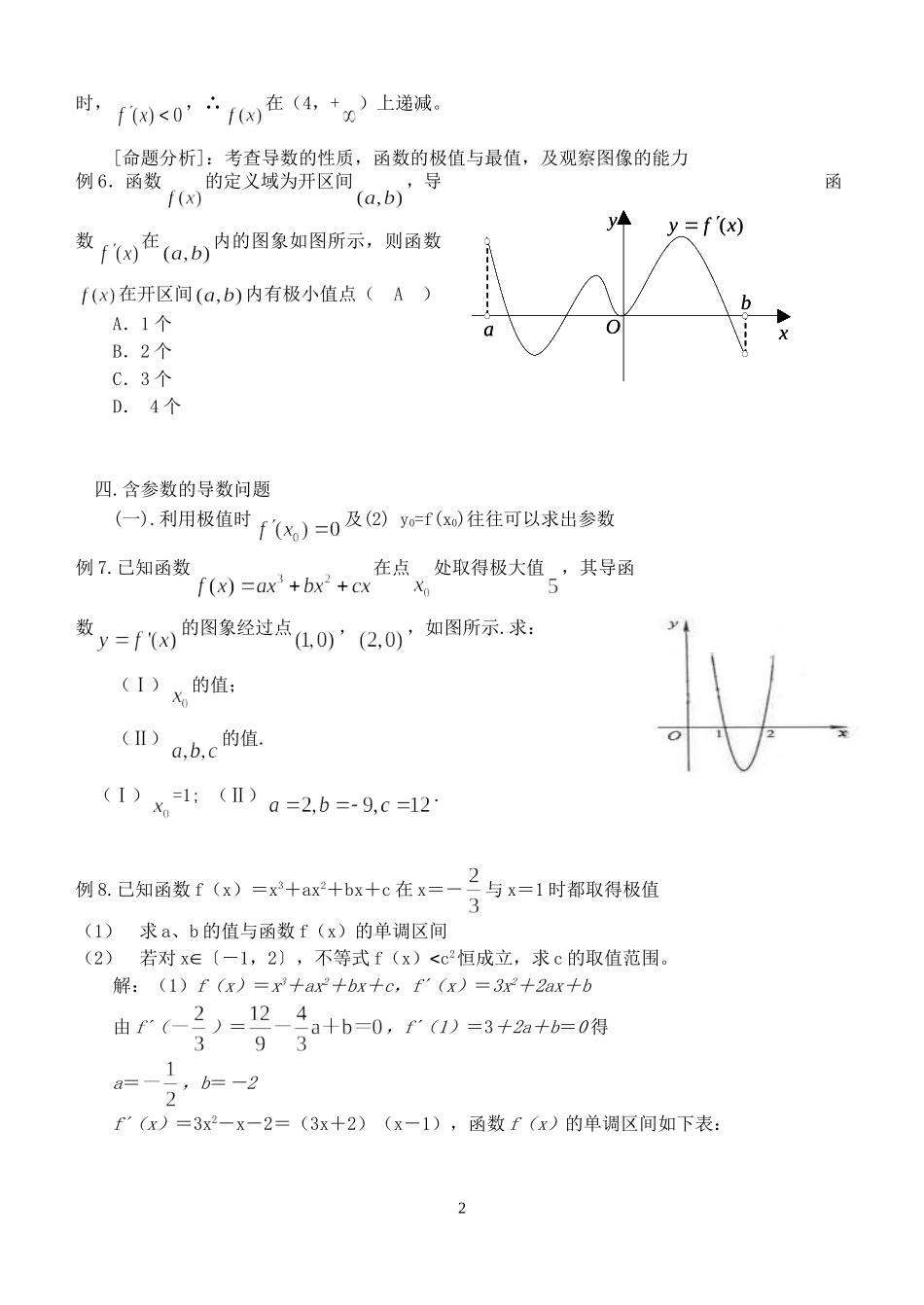
高三数学导数专题一、导数的定义及运用f(x)=例1．设函数f(x)在处可导，则等于（）A．B．C．D．二、导数与切线：y=f(x)上一点M（x0,y0）处的切线（1）斜率k=f/(x0)(2)y0=f(x0)(3)M（x0,y0）在切线上例2．（理）设，则它与x轴交点处的切线的方程为______________。（文）P是抛物线上的点，若过点P的切线方程与直线垂直，则过P点处的切线方程是____________。三、导数与单调性、极值(1).k=>0对应的区间为f(x)的单调增区间；（2）.k=<0对应的区间为f(x)的单调减区间；(3).k==0解得的x=x0可能是极值例3．((理)函数y=x-sinx,的最大值是(C)A.-1B.-1C.D.+1(文).为上为增函数,则a的取值范围为_________例4.f(x)=是否有极值?例5．已知函数，其导函数的图象如右图，则：(C)A．在(-，0)上为减函数B．在x=0处取得最大值C．在（4，+）上为减函数D．在x=2处取得最小值[思路分析]：由导函数的性质知，递增，递减。从图像上知，当x>41时，，∴在（4，+）上递减。[命题分析]：考查导数的性质，函数的极值与最值，及观察图像的能力例6．函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点（A）A．1个B．2个C．3个D．4个四.含参数的导数问题(一).利用极值时及(2)y0=f(x0)往往可以求出参数例7.已知函数在点处取得极大值，其导函数的图象经过点，，如图所示.求：（Ⅰ）的值；（Ⅱ）的值.（Ⅰ）=1;（Ⅱ）.例8.已知函数f（x）＝x3＋ax2＋bx＋c在x＝－与x＝1时都取得极值（1）求a、b的值与函数f（x）的单调区间（2）若对x〔－1，2〕，不等式f（x）c2恒成立，求c的取值范围。解：（1）f（x）＝x3＋ax2＋bx＋c，f（x）＝3x2＋2ax＋b由f（）＝，f（1）＝3＋2a＋b＝0得a＝，b＝－2f（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：2abxy)(xfyOabxy)(xfyOx（－，－）－（－，1）1（1，＋）f（x）＋0－0＋f（x）极大值极小值所以函数f（x）的递增区间是（－，－）与（1，＋）递减区间是（－，1）（2）f（x）＝x3－x2－2x＋c，x〔－1，2〕，当x＝－时，f（x）＝＋c为极大值，而f（2）＝2＋c，则f（2）＝2＋c为最大值。要使f（x）c2（x〔－1，2〕）恒成立，只需c2f（2）＝2＋c解得c－1或c2(二).根据单调性求参数范围或分类讨论参数来判断单调区间或极值例9.已知函数y=x3+ax2+bx在[0，2]上为单调递增，在[2，3]上单调递减，b的范围_____________例10．已知函数，其中为参数，且．（1）当时，判断函数是否有极值；（2）要使函数的极小值大于零，求参数的取值范围；无极值；例11.已知向量在区间（－1，1）上是增函数，求t的取值范围.解：依定义故要使在区间（－1，1）上恒成立(三)导论极值及根的存在情况例12.（1）求函数y=x3-3ax+2(a>0)3的极值.（2）研究方程x3-3ax+2=0(a>0)何时有三个不同的实根？何时有唯一的根练习题：1．函数f(x)=x4-x在点P处的切线平行于直线3x-y=0,则点P的坐标为（D）A.(1,3)B.(1,-3)C.D.(1,0)2.(理)函数f(x)=x-ex在点P处的切线平行于x轴，则点P的坐标为（D）A.(1.1-e)B.(1,e)C.(0,e)D.(0,-1)3.若f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值，则a的取值范围是（C）A.或B.C.a>2或a<-1D.4.已知是R上的单调增函数，则b的取值范围是（D）A.b<-1或b>2B.或C.-10a...