高三数学周练试题11 文-人教版高三全册数学试题VIP免费

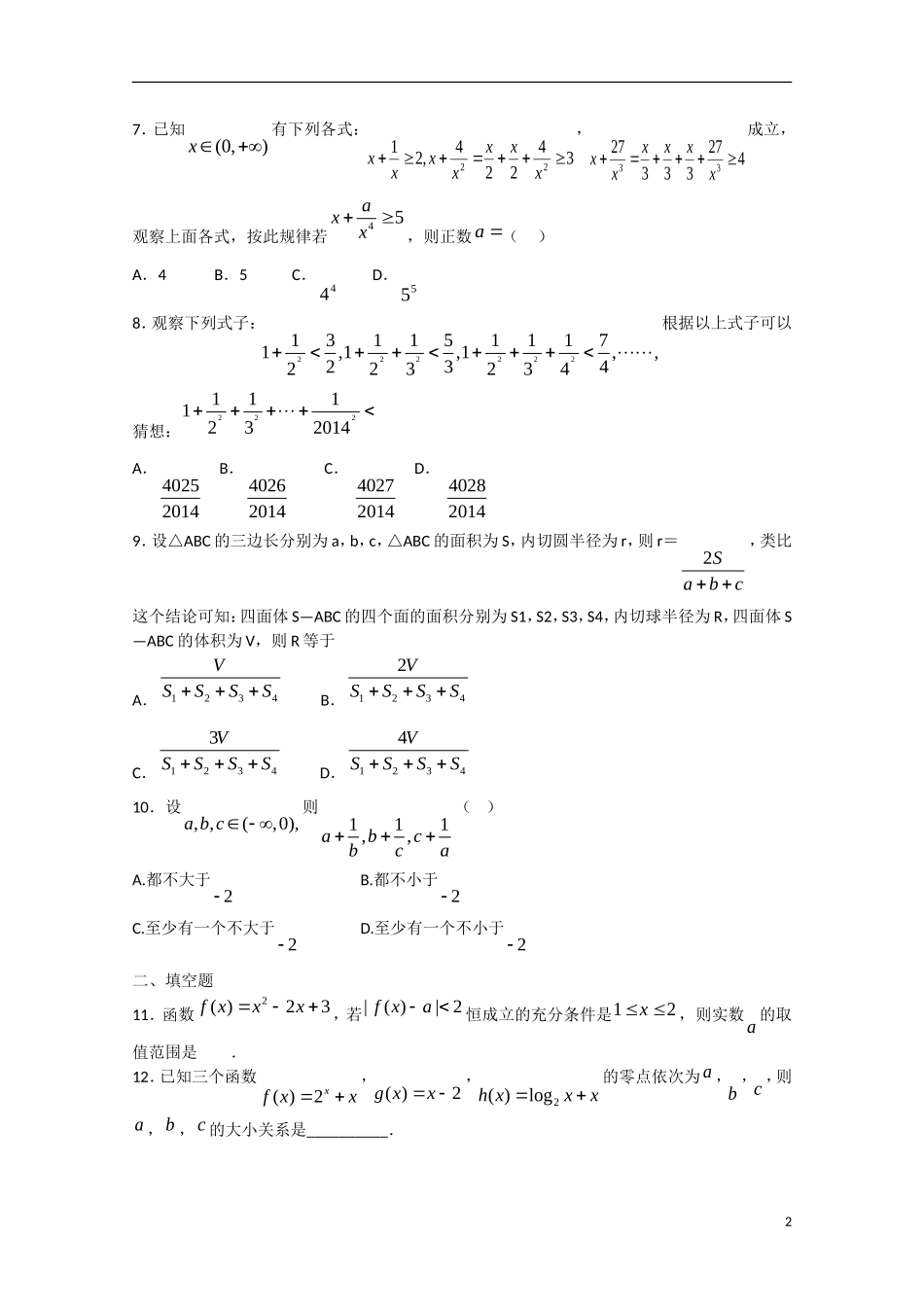
西安高新一中2015届文科数学周练（11）满分：150分时间：120分钟学号：班级：高三班姓名：成绩:一、选择题1．若关于x的不等式02caxx的解集为{|21}xx，且函数223cxmxaxy在区间)1,21(上不是单调函数，则实数m的取值范围为（）A．)3,3(B．]3,3[C．),3()2,(D．),3(]2,(2．若变量,xy满足约束条件211yxxyy，则2zxy的最大值为（）A．52B．0C．53D．523．设实数1,1ba，有如下四个结论：①若,3ln2lnbbaa则ba；②若,3ln2lnbbaa则ba；③若,3ln2lnbbaa则ba；④若,3ln2lnbbaa则ba．则下列命题成立的是（）A．①④B．②③C．①③D．②④4．若实数,xy满足不等式组,01,032,5yxyxy则yxz2的最大值是（）A．15B．14C．11D．105．若不等式08322＜kxkx对一切实数x都成立，则k的取值范围为（）A.)0,3(B.0,3C.0,3D.]0,3(6．已知,2log2,)21(,252.02.1cba则cba,,的大小关系为（）A．cabB．bacC．abcD．acb17．已知(0,)x有下列各式：34224,2122xxxxxxx，4273332733xxxxxx成立，观察上面各式，按此规律若45axx，则正数a（）A．4B．5C．44D．558．观察下列式子：2222221311511171,1,1,,234223234根据以上式子可以猜想：2221111232014A．40252014B．40262014C．40272014D．402820149．设△ABC的三边长分别为a，b，c，△ABC的面积为S，内切圆半径为r，则r＝2Sabc，类比这个结论可知：四面体S—ABC的四个面的面积分别为S1，S2，S3，S4，内切球半径为R，四面体S—ABC的体积为V，则R等于A．1234VSSSSB．12342VSSSSC．12343VSSSSD．12344VSSSS10．设,,(,0),abc则111,,abcbca（）A.都不大于2B.都不小于2C.至少有一个不大于2D.至少有一个不小于2二、填空题11．函数32)(2xxxf，若2|)(|axf恒成立的充分条件是21x，则实数a的取值范围是．12．已知三个函数xxfx2)(，2)(xxg，xxxh2log)(的零点依次为a，b，c，则a，b，c的大小关系是__________．213．36的所有正约数之和可按如下方法得到：因为2236=23，所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91（参照上述方法，可求得200的所有正约数之和为.14．在平面直角坐标系xOy中，已知圆5cos1:5sin2xCy（为参数）和直线46:32xtlyt（t为参数），则直线l被圆C所截得弦长为.三、解答题15．已知命题p：函数xay)1(在R上单调递增；命题q：不等式13axx的解集为R，若qp为真，qp为假，求实数a的取值范围．16．已知函数()|21||23|fxxx（1）求不等式()6fx的解集；（2）若关于x的不等式()|1|fxa的解集非空，求实数a的取值范围．317．解关于x的不等式3log22log1(01)aaxxaa且18．已知函数2111axbfxfx在点，的切线方程为30xy.（1）求函数fx的解析式；（2）设lngxx，求证：1,gxfxx在上恒成立；（3）已知22lnln20baaabbaab，求证：.19．（1）已知45x，求函数54124xxy的最大值；（2）已知0,0yx，且191yx，求yx的最小值．420．某工厂生产A、B两种产品，计划每种产品的生产量不少于15千克，已知生产A产品1千克要用煤9吨，电力4千瓦，3个工作日；生产B产品1千克要用煤4吨，电力5千瓦，10个工作日。又知生产出A产品1千克可获利7万元，生产出B产品1千克可获利12万元，现在工厂只有煤360吨，电力200千瓦，300个工作日，（1）列出满足题意的不等式组，并画图；（2）在这种情况下,生产A、B产品各多少千克能获得最大经济效益.参考答案1．A【解析】由不等式02caxx的解集为{|21}xx，02caxx的两根为1,2，可求得2,1ca，由函数123xmxxy在)1,21(上不是单调函数，可知01232m...