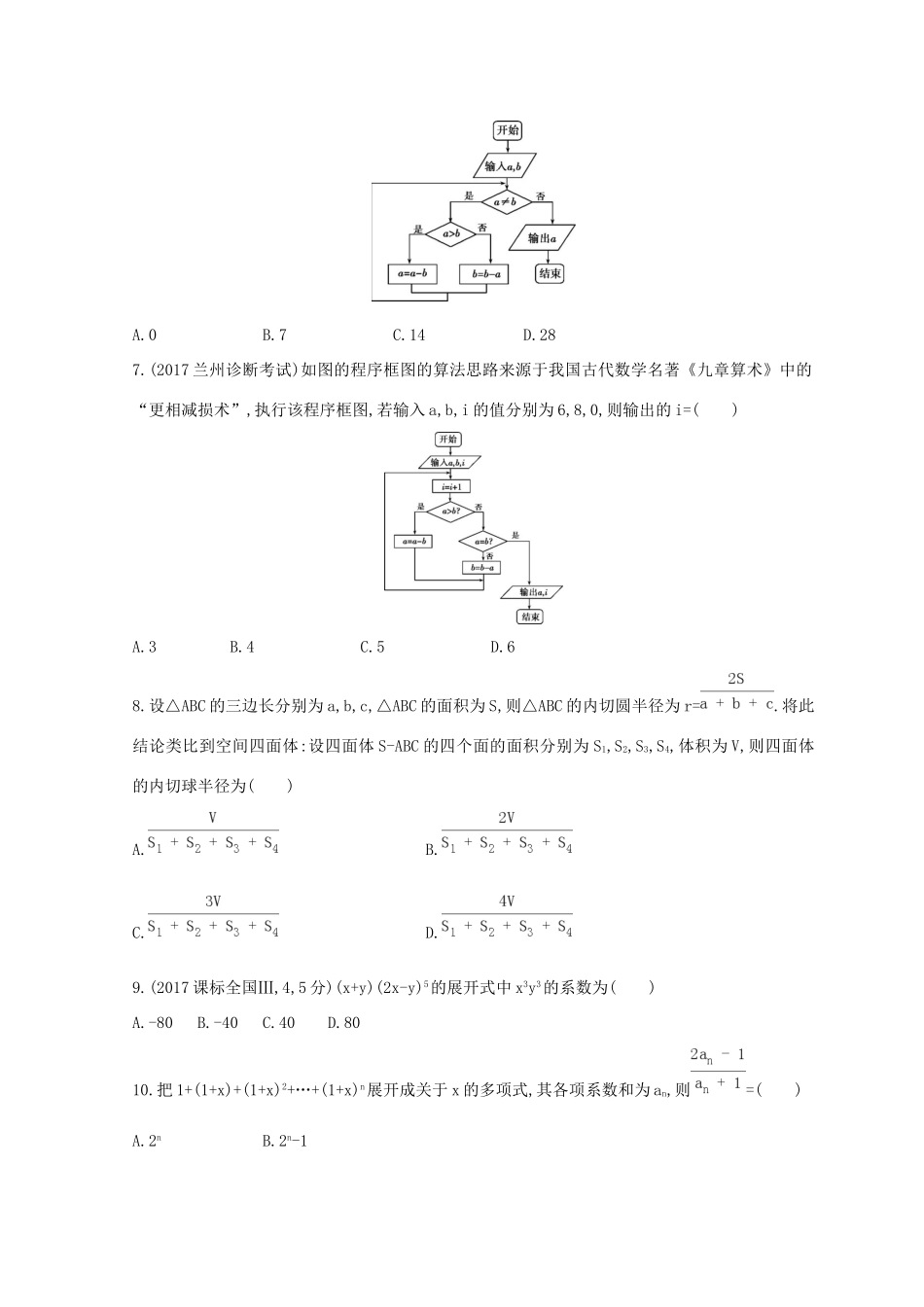
第4讲算法、推理与证明、计数原理A组基础题组1.设M,N是两个非空集合,定义M⊗N={(a,b)|a∈M,b∈N},若P={0,1,2,3},Q={1,2,3,4,5},则P⊗Q中元素的个数是()A.4B.9C.20D.242.(2017课标全国Ⅱ,7,5分)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩3.(2017成都第一次诊断性检测)执行如图所示的程序框图,如果输出的结果为0,那么输入的x为()A.B.-1或1C.1D.-14.在二项式的展开式中恰好第5项的二项式系数最大,则展开式中含x2项的系数是()A.-56B.-35C.35D.565.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有()A.60种B.63种C.65种D.66种6.(2017贵州适应性考试)执行如图所示的程序框图,如果输入的a,b的值分别为56,140,则输出的a=()A.0B.7C.14D.287.(2017兰州诊断考试)如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出的i=()A.3B.4C.5D.68.设△ABC的三边长分别为a,b,c,△ABC的面积为S,则△ABC的内切圆半径为r=.将此结论类比到空间四面体:设四面体S-ABC的四个面的面积分别为S1,S2,S3,S4,体积为V,则四面体的内切球半径为()A.B.C.D.9.(2017课标全国Ⅲ,4,5分)(x+y)(2x-y)5的展开式中x3y3的系数为()A.-80B.-40C.40D.8010.把1+(1+x)+(1+x)2+…+(1+x)n展开成关于x的多项式,其各项系数和为an,则=()A.2nB.2n-1C.2D.2-11.(2017福州综合质量检测)执行如图所示的程序框图,若输入的m=168,n=112,则输出的k,m的值分别为()A.4,7B.4,56C.3,7D.3,5612.(2017湖南湘中名校高三联考)执行如图所示的程序框图,如果运行结果为5040,那么判断框中应填入()A.k<6?B.k<7?C.k>6?D.k>7?13.(2017兰州高考实战模拟)观察下列式子:1,1+2+1,1+2+3+2+1,1+2+3+4+3+2+1,…,由以上可推测出一个一般性结论:对于n∈N*,则1+2+…+n+…+2+1=.14.(2017昆明教学质量检测)某小区一号楼共有7层,每层只有1家住户,已知任意相邻两层楼的住户在同一天至多一家有快递,且任意相邻三层楼的住户在同一天至少一家有快递,则在同一天这7家住户有无快递的可能情况共有种.15.(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=.16.(2017张掖第一次诊断考试)设f(x)是的展开式中的中间项,若f(x)≤mx在区间上恒成立,则实数m的取值范围是.B组提升题组1.如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依此规律A(8,2)为()……A.B.C.D.2.已知数列{an}是正项等差数列,若cn=,则数列{cn}也为等差数列.已知数列{bn}是正项等比数列,类比上述结论可得()A.若{dn}满足dn=,则{dn}也是等比数列B.若{dn}满足dn=,则{dn}也是等比数列C.若{dn}满足dn=(b1·2b2·3b3·…·nbn)1+2+3+…+n,则{dn}也是等比数列D.若{dn}满足dn=(b1···…·,则{dn}也是等比数列3.已知-的展开式中含x2与x3的项的系数绝对值之比为1∶6,则a2+b2的最小值为()A.6B.9C.12D.184.(2017广东五校协作体第一次诊断考试)已知函数f(x)=ax3+x2在x=-1处取得极大值,记g(x)=.执行如图所示的程序框图,若输出的结果S>,则判断框中可以填入的关于n的判断条件是()A.n≤2016?B.n≤2017?C.n>2016?D.n>2017?5.(2017武汉武昌调研考试)若的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是()A.-270B.270C.-90D.906.现需编制一个八位的序号,规定如下:①序号由4个数字和2个x、1个y、1个z组成;②2个x不能连续出现,且y在z的前面;③数字在0,1,2,…,9之间任选,可重复,且4个数字之积为8,则符合条件的不同序号的种数为()A.12600B.6300C.5040D.25207.我们可以用随机数法估计π的值,如图所示的程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数),若输出的结果为521,则由此可估计π的近似值为()A.3.119B.3.126C.3.132D.3.1518.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉...