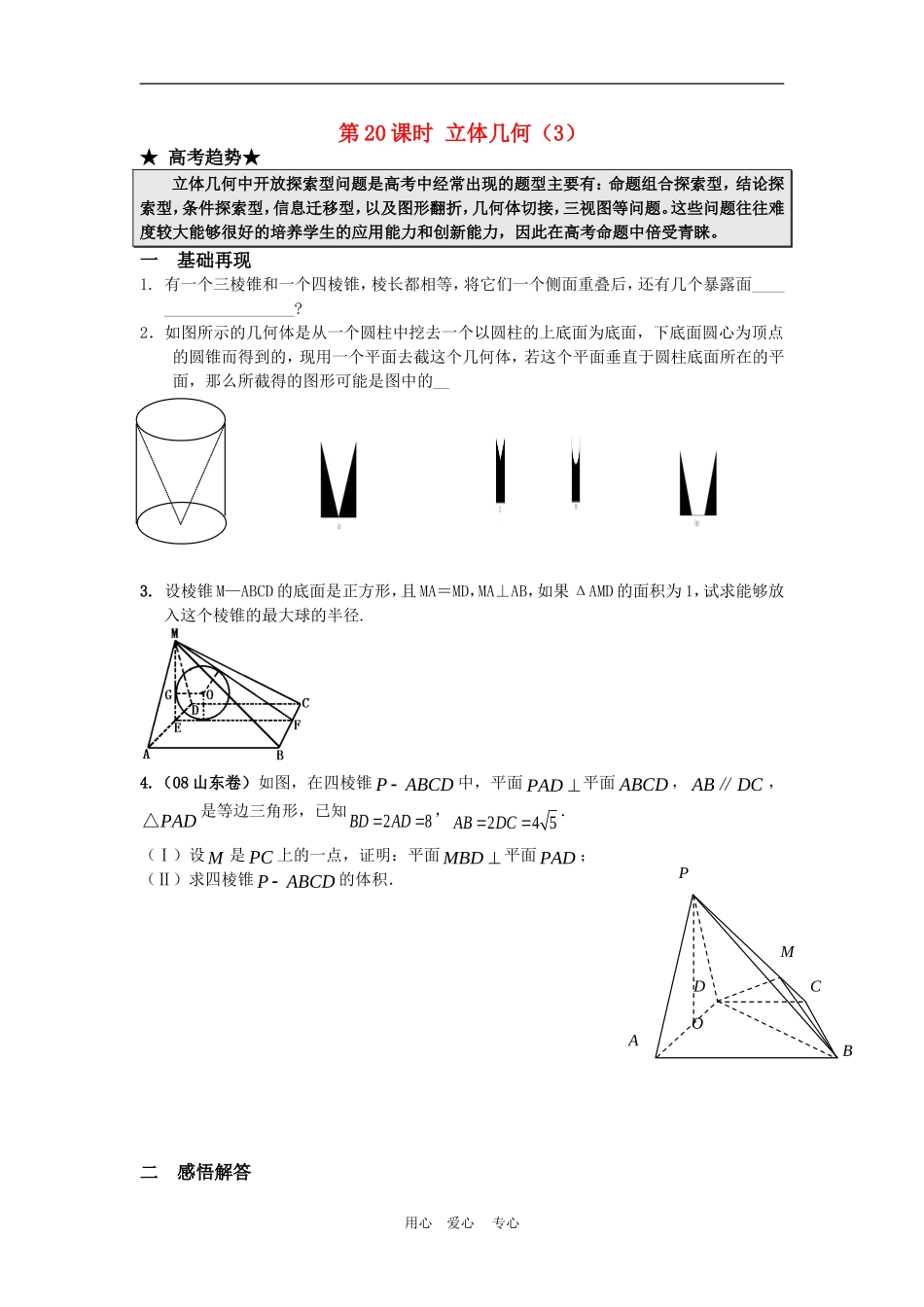
第20课时立体几何(3)★高考趋势★立体几何中开放探索型问题是高考中经常出现的题型主要有:命题组合探索型,结论探索型,条件探索型,信息迁移型,以及图形翻折,几何体切接,三视图等问题。这些问题往往难度较大能够很好的培养学生的应用能力和创新能力,因此在高考命题中倍受青睐。一基础再现1.有一个三棱锥和一个四棱锥,棱长都相等,将它们一个侧面重叠后,还有几个暴露面____________________?2.如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的,现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么所截得的图形可能是图中的__3.设棱锥M—ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.4.(08山东卷)如图,在四棱锥PABCD中,平面PAD平面ABCD,ABDC∥,PAD△是等边三角形,已知28BDAD,245ABDC.(Ⅰ)设M是PC上的一点,证明:平面MBD平面PAD;(Ⅱ)求四棱锥PABCD的体积.二感悟解答用心爱心专心ABCMPDO1.解析:有5个暴露面.如图所示,过V作VS′∥AB,则四边形S′ABV为平行四边形,有∠S′VA=∠VAB=60°,从而ΔS′VA为等边三角形,同理ΔS′VD也是等边三角形,从而ΔS′AD也是等边三角形,得到以ΔVAD为底,以S′与S重合.这表明ΔVAB与ΔVSA共面,ΔVCD与ΔVSD共面,故共有5个暴露面.2.(1)(3)3.解析:∵AB⊥AD,AB⊥MA,∴AB⊥平面MAD,由此,面MAD⊥面AC.记E是AD的中点,从而ME⊥AD.∴ME⊥平面AC,ME⊥EF,设球O是与平面MAD、AC、平面MBC都相切的球.不妨设O∈平面MEF,于是O是ΔMEF的内心.设球O的半径为r,则r=MFEMEFSMEF△2,设AD=EF=a,∵SΔAMD=1.∴ME=a2.MF=22)2(aa,则r=22)2(22aaaa≤2222=2-1,当且仅当a=a2,即a=2时,等号成立.∴当AD=ME=2时,满足条件的球最大半径为2-1.4.(Ⅰ)证明:在ABD△中,由于4AD,8BD,45AB,所以222ADBDAB.故ADBD.又平面PAD平面ABCD,平面PAD平面ABCDAD,BD平面ABCD,所以BD平面PAD,又BD平面MBD,故平面MBD平面PAD.(Ⅱ)解:过P作POAD交AD于O,由于平面PAD平面ABCD,所以PO平面ABCD.因此PO为四棱锥PABCD的高,又PAD△是边长为4的等边三角形.因此34232PO.在底面四边形ABCD中,ABDC∥,2ABDC,所以四边形ABCD是梯形,在RtADB△中,斜边AB边上的高为4885545,此即为梯形ABCD的高,所以四边形ABCD的面积为2545852425S.故124231633PABCDV.三范例剖析用心爱心专心ABCDD1C1B1A1例1直棱柱1111ABCDABCD中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,222ABADCD.(Ⅰ)求证:AC⊥平面BB1C1C;(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.例2如图,在四棱锥PABCD中,侧面PAD底面ABCD,侧棱PAPD,底面ABCD是直角梯形,其中//BCAD,090BAD,3ADBC,O是AD上一点.(Ⅰ)若//CDPBO平面,试指出点O的位置;(Ⅱ)求证:PABPCD平面平面.例3在正方体1111ABCDABCD中,已知E、F、G分别是棱AB、AD、11DA的中点.(1)求证:BG//平面1AEF;(2)若P为棱1CC上一点,求当1CPPC等于多少时,平面1AEF平面EFP?用心爱心专心ABCDA1D1C1B1GEFP(第3题)OPDCBA第2题四巩固训练1.正四棱柱ABCD–A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R–PQMN的体积是__________2.如图所示,正方体ABCD—A1B1C1D1中,1,EFACEFAD则EF和BD1的关系是3.如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.4.如图,四面体C—ABD,CB=CD,AB=AD,∠BAD=90°.E、F分别是BC、AC的中点.(Ⅰ)求证:AC⊥BD;(Ⅱ)如何在AC上找一点M,使BF∥平面MED?并说明理由;(Ⅲ)若CA=CB,求证:点C在底面ABD上的射影是线段BD的中点.用心爱心专心BCADEFM