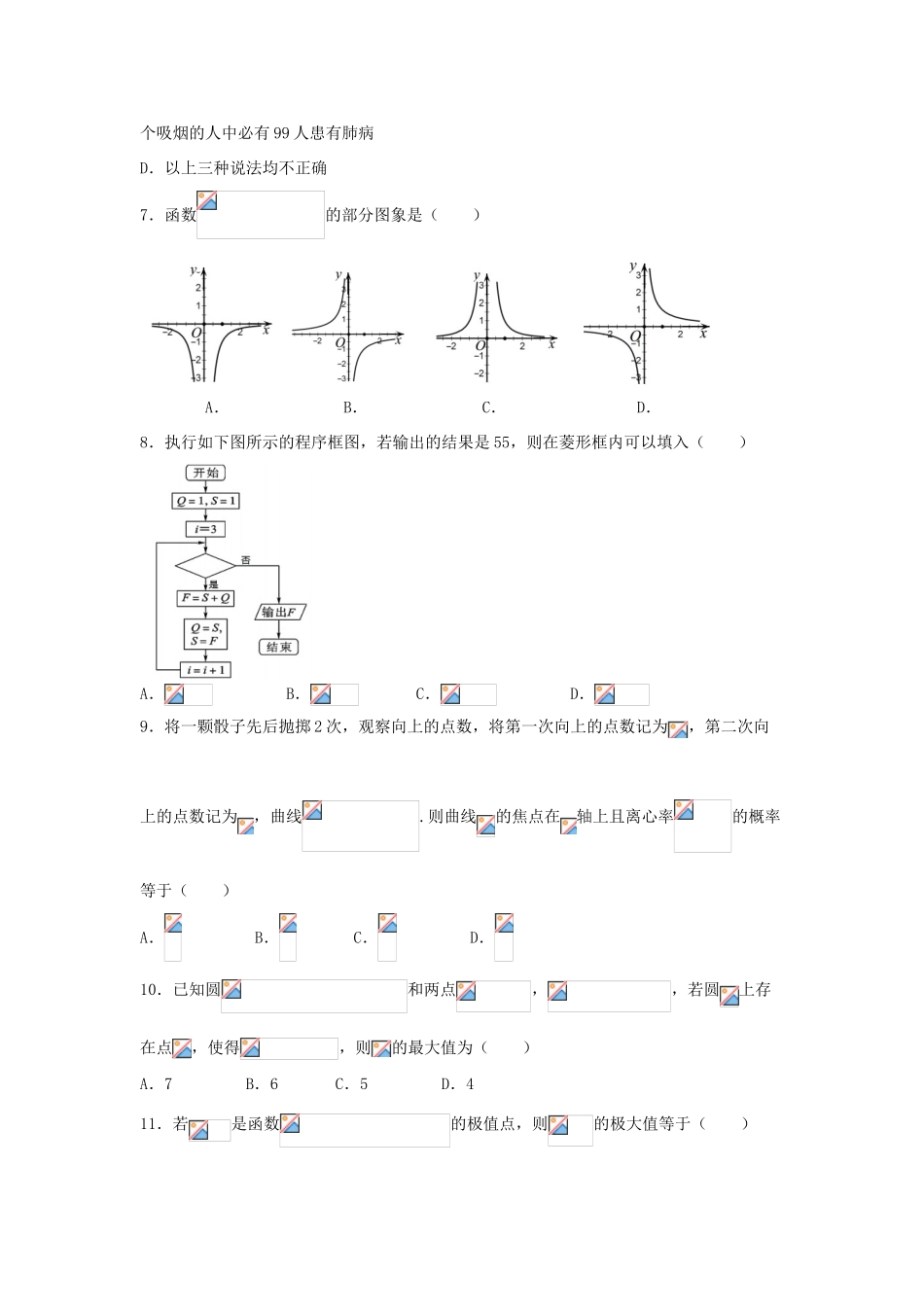
四川省绵阳南山中学2018届高三数学二诊热身考试试题文第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则集合中元素个数是()A.0B.1C.2D.42.已知复数,则所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.“”是“直线和直线互相垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.下列4个图从左到右位次是四位同学甲、乙、丙、丁的五能评价雷达图:在从他们四人中选一位发展较全面的学生,则应该选择()A.甲B.乙C.丙D.丁5.若,则()A.B.C.D.6.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是()A.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病C.若的观测值为,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病D.以上三种说法均不正确7.函数的部分图象是()A.B.C.D.8.执行如下图所示的程序框图,若输出的结果是55,则在菱形框内可以填入()A.B.C.D.9.将一颗骰子先后抛掷2次,观察向上的点数,将第一次向上的点数记为,第二次向上的点数记为,曲线.则曲线的焦点在轴上且离心率的概率等于()A.B.C.D.10.已知圆和两点,,若圆上存在点,使得,则的最大值为()A.7B.6C.5D.411.若是函数的极值点,则的极大值等于()A.-1B.3C.D.12.已知是边长为2的正三角形,点为平面内一点,且,则的取值范围是()A.B.C.D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是.14.已知焦点在坐标轴上,中心是原点的双曲线的一条渐近线方程为,且经过点,则双曲线的焦点到渐近线的距离等于.15.函数是上的奇函数,,且对任意,有,则不等式的解集为.16.设抛物线的焦点为是抛物线上一点,的延长线与轴相交于点,若,则.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列的前项和是,且.(1)求数列的通项公式;(2)令,求数列前项的和.18.的内角的对边分别为,已知.(1)求角的大小;(2)若边上的高等于,求的值.19.某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以(单位:盒,)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.(1)根据直方图估计这个开学季内市场需求量的平均数;(2)将表示为的函数;(3)根据直方图估计利润不少于4000元的概率.20.已知椭圆的焦距为,且经过点.过点的斜率为的直线与椭圆交于两点,与轴交于点,点关于轴的对称点,直线交轴于点.(1)求的取值范围;(2)试问:是否为定值?若是,求出定值;否则,说明理由.21.已知函数,.(1)若函数与在处有相同的切线,求的值;(2)若,恒有成立,求实数的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系中,以原点为极点,轴的正半轴为极轴建立极坐标系.已知直线经过点,曲线.(1)求直线和曲线的直角坐标方程;(2)若点为曲线上任意一点,且点到直线的距离为,求的最小值.23.选修4-5:不等式选讲已知,函数.(1)若的最小值为-2,求实数的值;(2)若函数的图象与轴所围的图形的面积不大于6时,求的取值范围.参考答案一、选择题1-5:CACBB6-10:ADCDB11、12:DA二、填空题13.914.15.16.10三、解答题17.解:(1)由得,于是是等比数列.令得,所以.(2),于是数列是首项为0,公差为1的等差...