高三数学九月月考试题 理-人教版高三全册数学试题VIP免费

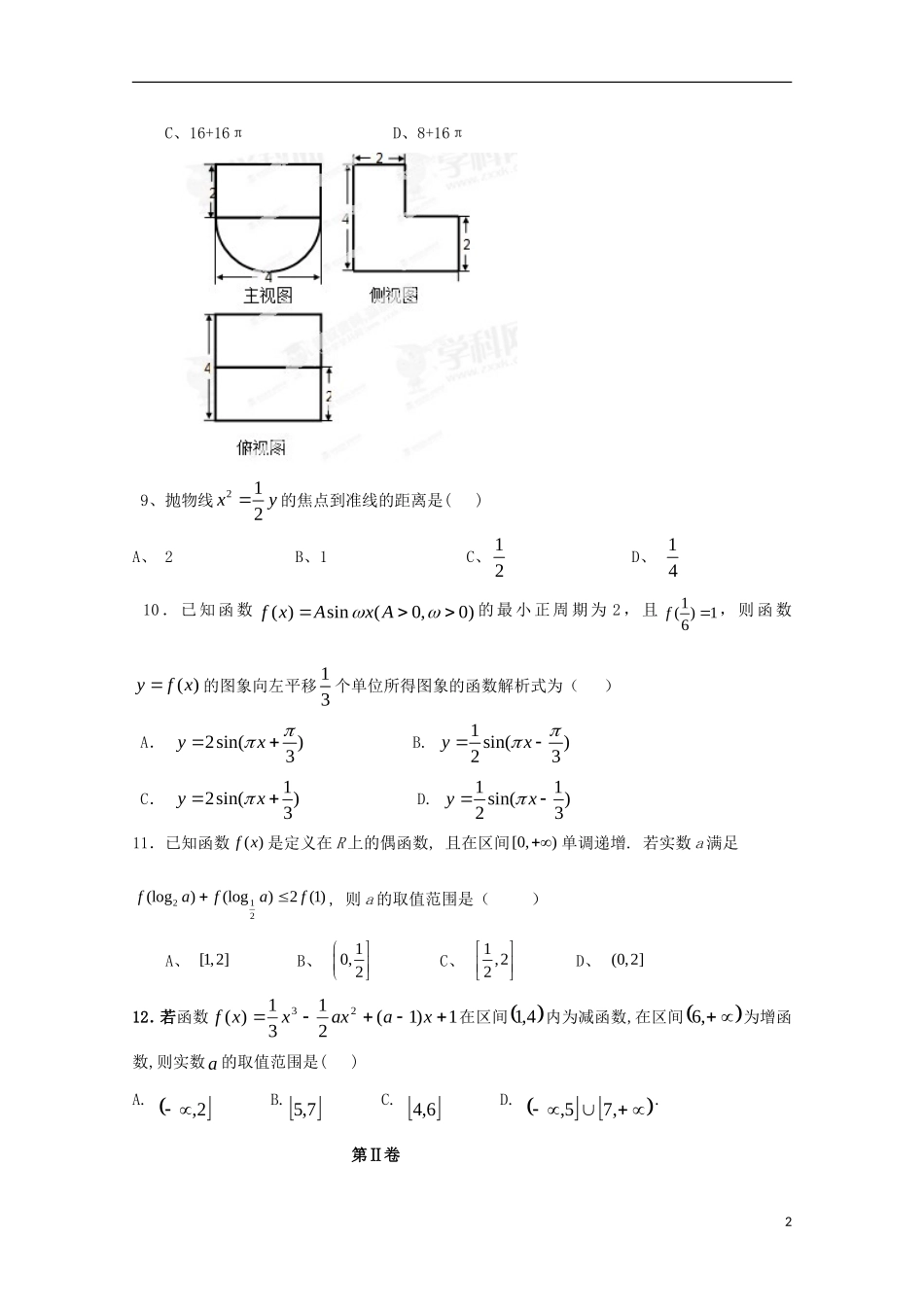
高三第一次月考理数试题一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．复数＝()A．－iB．＋iC．1－iD．1＋i2．已知集合A=｛x|x2－2x＞0｝，B=｛x|－＜x＜｝，则()A、A∩B=B、AB=RC、BAD、AB3．1a是“直线012:1yaxl与直线04)1(:2yaxl平行”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4．61xx的二项展开式中的常数项为.A、-4B、-3C、-2D、155．右图是一个算法框图，则输出的k的值是()A.3B.4C.5D.66．若x，y∈R，且则z＝x＋2y的最小值等于()A．2B．3C．5D．97.设(x1，y1)，(x2，y2)，…，(xn，yn)是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图1－4)，以下结论中正确的是()图1－4A．x和y的相关系数为直线l的斜率B．x和y的相关系数在0到1之间C．当n为偶数时，分布在l两侧的样本点的个数一定相同D．直线l过点(，)8．、某几何函数的三视图如图所示，则该几何的体积为()A、16+8πB、8+8π1C、16+16πD、8+16π9、抛物线212xy的焦点到准线的距离是()A、2B、1C、12D、1410．已知函数()sin(0,0)fxAxA的最小正周期为2，且1()16f，则函数()yfx的图象向左平移13个单位所得图象的函数解析式为（）A．2sin()3yxB.1sin()23yxC．12sin()3yxD.11sin()23yx11．已知函数()fx是定义在R上的偶函数,且在区间[0,)单调递增.若实数a满足212(log)(log)2(1)faffa,则a的取值范围是（）A、[1,2]B、10,2C、1,22D、(0,2]12．若函数1)1(2131)(23xaaxxxf在区间4,1内为减函数,在区间,6为增函数,则实数a的取值范围是()A.2,B.7,5C.6,4D.,75,.第Ⅱ卷2二、填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上）13、从1，2，3，4，5中任意取出两个不同的数，其和为5的概率为________.14、函数y=()fx的图象在点(3,(3))Pf处的切线方程为2yx,()fx为()fx的导函数，则(3)(3)ff15、已知函数12(0)()2(0)xxxfxx则(9)ff_____.16、计算定积分dxxx112)sin(___________。三．解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（本小题满分12分）已知数列{}na是公差不为零的等差数列，23a=，且5a是48,aa的等比中项.（Ⅰ）求数列{}na的通项公式；（Ⅱ）设nS为数列{}na的前n项和，求使nnaS=成立的所有n的值.18.(本小题满分12分)如图，在四棱锥中ABCDP中，底面ABCD为菱形，60BAD，Q为AD的中点.（I）若PDPA，求证：平面PQB平面PAD；（II）若平面PAD平面ABCD，且2ADPDPA，求四棱锥ABCDP的体积.3BACDPQ19．(本小题满分12分)电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图．图1－6将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．(1)根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？非体育迷体育迷合计男ab女cd=1055合计n(2)将上述调查所得到的频率视为概率．现在从该地区大量电视观众中．采用随机抽样方法每次抽取1名观众，抽取3次．记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的，求X的分布列，期望E(X)和方差D(X)．附：χ2＝为样本容量）（其中dcbandbcadcbabcadn))()()(()(2P(χ2≥k)0.050.01k3.8416.63520（本小题满分12分）已知函数f（x）=xxln82，x∈，（I）求f（x）的最大值与最小值；（II）若f（x）＜4﹣at于任意的x∈，t∈恒成立，求实数a的取值范围．21．（本题满分12分）平面直角坐标系xOy中，过椭圆M：22221(0)xyabab右焦点的直线30xy交M于A,B两点，P为AB的中点，且OP的斜率为12.(Ι)求M的方程；4（Ⅱ）C,D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形面积的最大值请考生在第22...