高三数学九月月考试题 文-人教版高三全册数学试题VIP免费

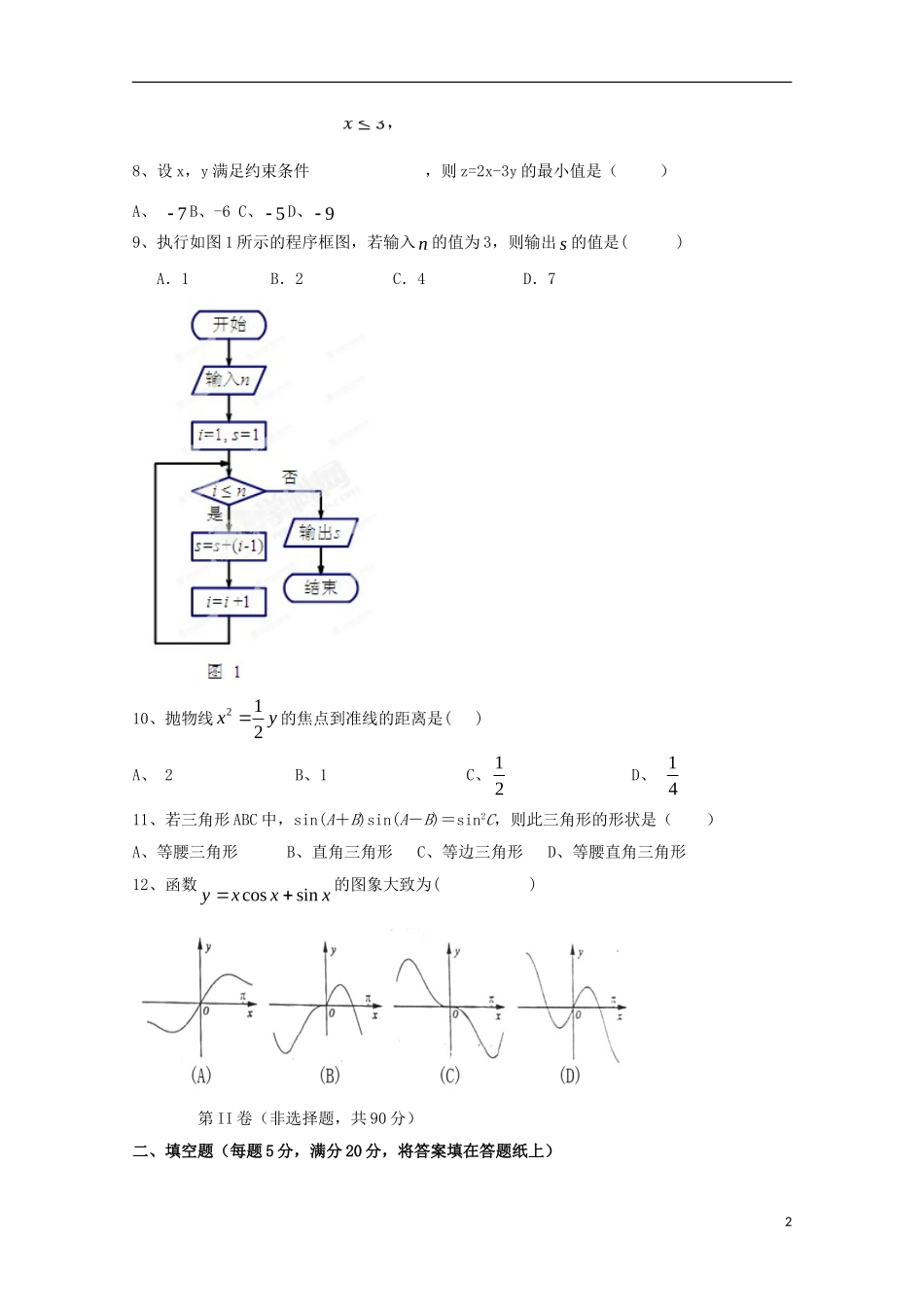
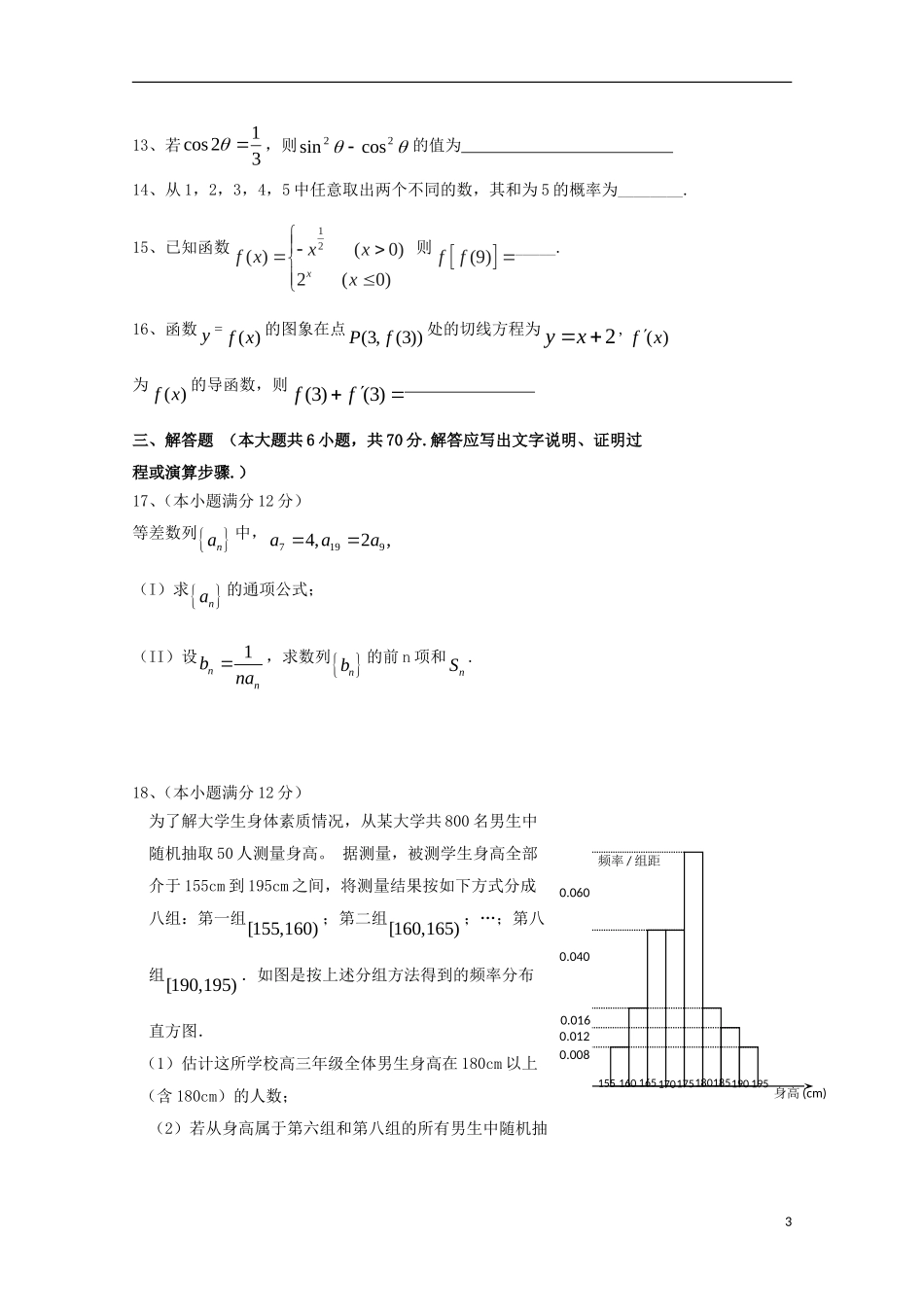
高三第一次月考文数试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、设集合1,2,3,4,5,U集合1,2A，则ACu=（）（A）1,2（B）3,4,5（C）1,2,3,4,5（D）2、在复平面内，复数z满足Z=1+3i，则z的共轭复数对应的点位于（）A．第一象限Ｂ．第二象限C．第三象限Ｄ．第四象限3、下列函数中，在(0)，内单调递增，并且是偶函数的是（）A．2(1)yxB．cos1yxC．lg||2yxD．2xy4、已知向量(1,),(,2),ambm,若ab∥则实数m等于（）A、2B、2C、2或2D、05、设nS为等差数列na的前n项和，8374,2Saa，则9a=（）A、6B、4C、2D、26、某三棱锥的三视图如图2所示，则该三棱锥的体积是（）A．16B．13C．23D．1图21俯视图侧视图正视图217、函数lg(1)()1xfxx的定义域是（）A．(1,)B．[1,)C．(1,1)(1,)D．[1,1)(1,)18、设x，y满足约束条件，则z=2x-3y的最小值是（）A、7B、-6C、5D、99、执行如图1所示的程序框图，若输入n的值为3，则输出s的值是()A．1B．2C．4D．710、抛物线212xy的焦点到准线的距离是()A、2B、1C、12D、1411、若三角形ABC中，sin(A＋B)sin(A－B)＝sin2C，则此三角形的形状是（）A、等腰三角形B、直角三角形C、等边三角形D、等腰直角三角形12、函数xxxysincos的图象大致为()第II卷（非选择题，共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）213、若312cos，则22cossin的值为14、从1，2，3，4，5中任意取出两个不同的数，其和为5的概率为________.15、已知函数12(0)()2(0)xxxfxx则(9)ff_____.16、函数y=()fx的图象在点(3,(3))Pf处的切线方程为2yx,()fx为()fx的导函数，则(3)(3)ff三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17、（本小题满分12分）等差数列na中，71994,2,aaa（I）求na的通项公式；（II）设1nnbna，求数列nb的前n项和nS.18、（本小题满分12分）为了解大学生身体素质情况，从某大学共800名男生中随机抽取50人测量身高。据测量，被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155,160)；第二组[160,165)；…；第八组[190,195)．如图是按上述分组方法得到的频率分布直方图．（1）估计这所学校高三年级全体男生身高在180cm以上（含180cm）的人数；（2）若从身高属于第六组和第八组的所有男生中随机抽30.0081851801751701651601551951900.0400.0160.0120.060频率/组距身高(cm)取两人，记他们的身高分别为,xy，求满足“||5xy”的事件的概率．19、（本小题满分12分）如图，在四棱锥中ABCDP中，底面ABCD为菱形，60BAD，Q为AD的中点.（I）若PDPA，求证：平面PQB平面PAD；（II）若平面PAD平面ABCD，且2ADPDPA，求四棱锥ABCDP的体积.20、（本小题满分12分）设椭圆22221(0)xyabab的左焦点为F,离心率为33,过点F且与x轴垂直的直线被椭圆截得的线段长为433.(Ⅰ)求椭圆的方程;(Ⅱ)设A,B分别为椭圆的左右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若··8ACDBADCB�,求k的值.21、（本小题满分12分）已知函数32=331.fxxaxx（I）当-2a时，讨论fx的单调性；（II）若2,x时，0fx，求a的取值范围.4BACDPQ请从下面所给的22、23、24三题中选定一题作答，多答按所答第一题评分请考生在（22）、（23）、（24）三题中任选一题作答，如果多做，则按所做的第一题记分22．（本小题满分10分）选修4－1：几何证明选讲如图所示，已知PA与圆O相切，A为切点，PBC为割线，弦,CDAPADBC∥、相交于E点，F为CE上一点，且2DEEFEC.（1）求证：PEDF；（2）求证：CEEBEFEP.23．（本小题满分10分）选修4—4：坐标系与参数方程已知直线l的参数方程为122322xtyt（t为参数），若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，曲线...