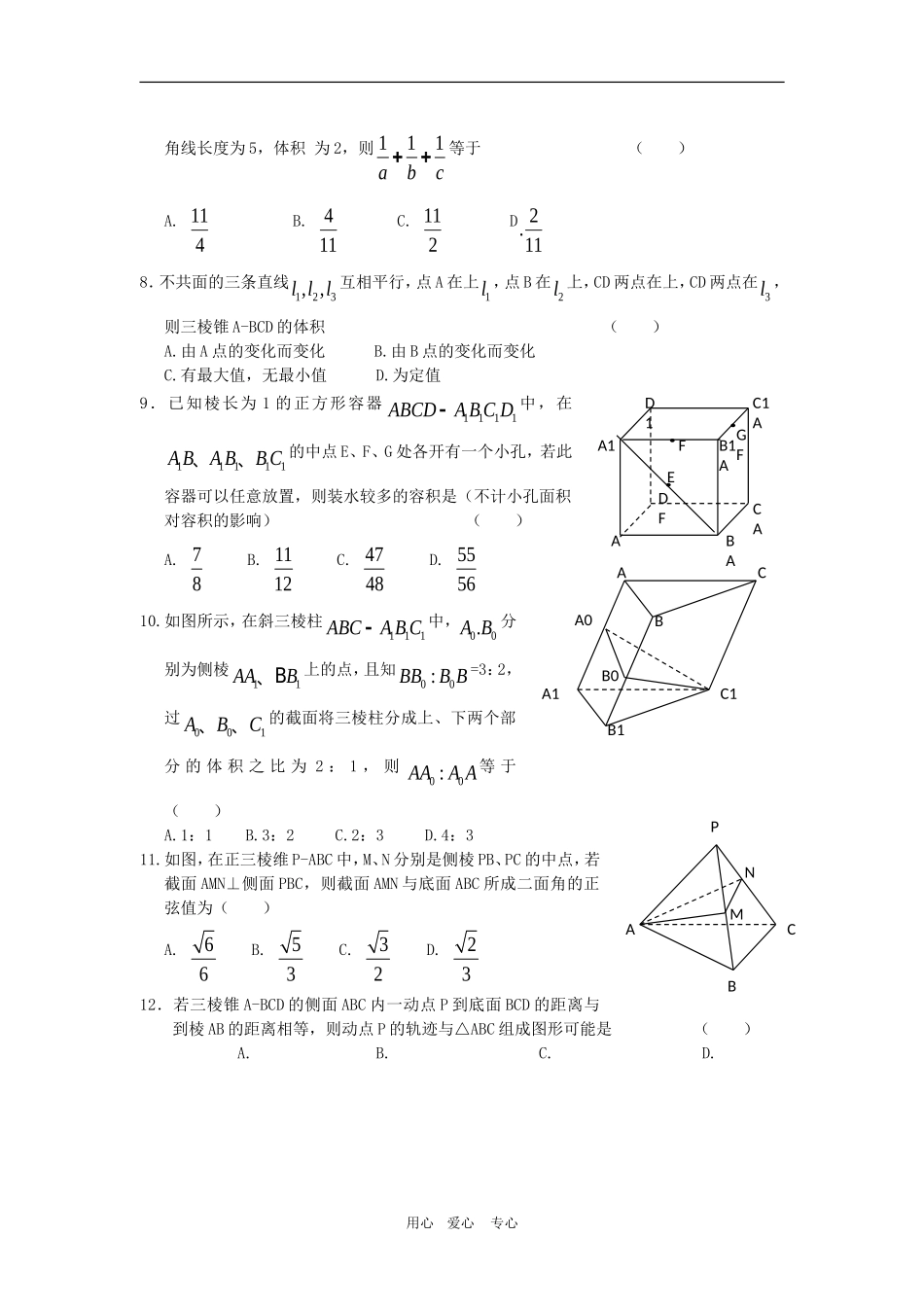
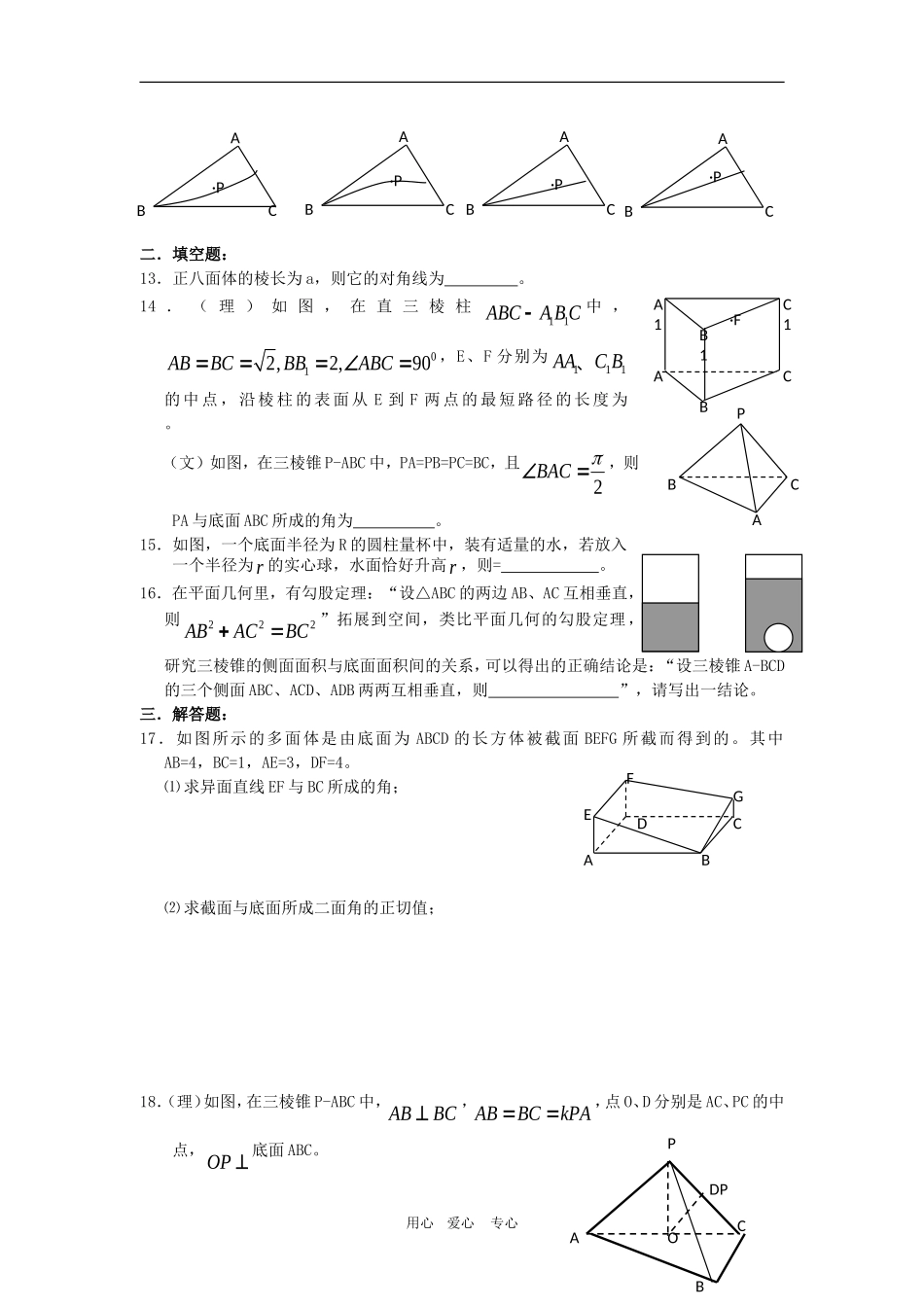
ABCDFE高三数学专题测试第八单元简单多面体一、选择题:1.给出下列命题:①有一条侧棱与底面两边垂直的棱柱是直棱柱;②底面为正多边形的棱柱为正棱柱;③顶点在底面上的射影到底面各顶点的距离相等的棱维是正棱锥;④A、B为球面上相异的两点,则通过A、B的大圆有且公有一个。其中正确命题的个数是()A.0个B.1个C.2个D.3个2.正四棱柱底面面积为M,对角面面积为N,其体积为()A.2NMB.2MNC.22NMD.22MN3.如图,一个封闭的长方体,它6个表面各标出A、B、C、D、E、F这6个字母中的1个字母,现放成下面3个不同位置,所看见的表面上的字母已标明,则字母A、B、C对面的字母分别是()A.D、E、FB.F、D、EC.E、F、DD.E、D、F4.已知一个半径为21的球中有一个各条棱长都相等,那么这个圆维轴截面顶角的内接正三棱柱,则这一正三棱柱的体积是()A.543B.483C.363D.2435.一个圆锥和一具半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥轴截面顶角的余弦值是()A.34B.45C.35D.356.如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形EFAB,2EF,则该多面体的体积为()A.33B.23C.43D.327.长方体的一个顶点上三条棱的长分别为a、b、c,若长方体所有棱的长度之和为24,一条对用心爱心专心BACDCBABBCE角线长度为5,体积为2,则111abc等于()A.114B.411C.112D2.118.不共面的三条直线123,,lll互相平行,点A在上1l,点B在2l上,CD两点在上,CD两点在3l,则三棱锥A-BCD的体积()A.由A点的变化而变化B.由B点的变化而变化C.有最大值,无最小值D.为定值9.已知棱长为1的正方形容器1111ABCDABCD中,在11111ABABBC、、的中点E、F、G处各开有一个小孔,若此容器可以任意放置,则装水较多的容积是(不计小孔面积对容积的影响)()A.78B.1112C.4748D.555610.如图所示,在斜三棱柱111ABCABC中,00.AB分别为侧棱11AAB、B上的点,且知00:BBBB=3:2,过001ABC、、的截面将三棱柱分成上、下两个部分的体积之比为2:1,则00:AAAA等于()A.1:1B.3:2C.2:3D.4:311.如图,在正三棱维P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则截面AMN与底面ABC所成二面角的正弦值为()A.66B.53C.32D.2312.若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等,则动点P的轨迹与△ABC组成图形可能是()A.B.C.D.用心爱心专心ABACADFA1B1AC1AD1FGFEACC1A1B1BA0B0ABCPNMPACBDPO二.填空题:13.正八面体的棱长为a,则它的对角线为。14.(理)如图,在直三棱柱11ABCABC中,012,2,90ABBCBBABC,E、F分别为111AACB、的中点,沿棱柱的表面从E到F两点的最短路径的长度为。(文)如图,在三棱锥P-ABC中,PA=PB=PC=BC,且2BAC,则PA与底面ABC所成的角为。15.如图,一个底面半径为R的圆柱量杯中,装有适量的水,若放入一个半径为r的实心球,水面恰好升高r,则=。16.在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则222ABACBC”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则”,请写出一结论。三.解答题:17.如图所示的多面体是由底面为ABCD的长方体被截面BEFG所截而得到的。其中AB=4,BC=1,AE=3,DF=4。⑴求异面直线EF与BC所成的角;⑵求截面与底面所成二面角的正切值;18.(理)如图,在三棱锥P-ABC中,ABBC,ABBCkPA,点O、D分别是AC、PC的中点,OP底面ABC。用心爱心专心FEGABCDABC·PABC·PABC·PABC·P·FA1C1B1ABCPBAC⑴求证:OD平面PAB;⑵当12k时,直线PA与平面PBC所成角的大小;⑶当k为何值时,O在平面PBC内的射影恰好为△PBC的重心?(文)如图,在三棱锥P-ABC中,1,2ABBCABBCPA,点O、D分别是AC、PC的中点,OP底面ABC,⑴求证:CD平面PAB;⑵求直线OD与平面PBC所成角的大小。19.如图,三棱锥P-ABC中,PA底面ABC,090,2,23BACPAABAC,以PA的直径的球和PB、PC分别交于11BC、,求11BC、两点的球面距离。用心爱心专心B1AA...