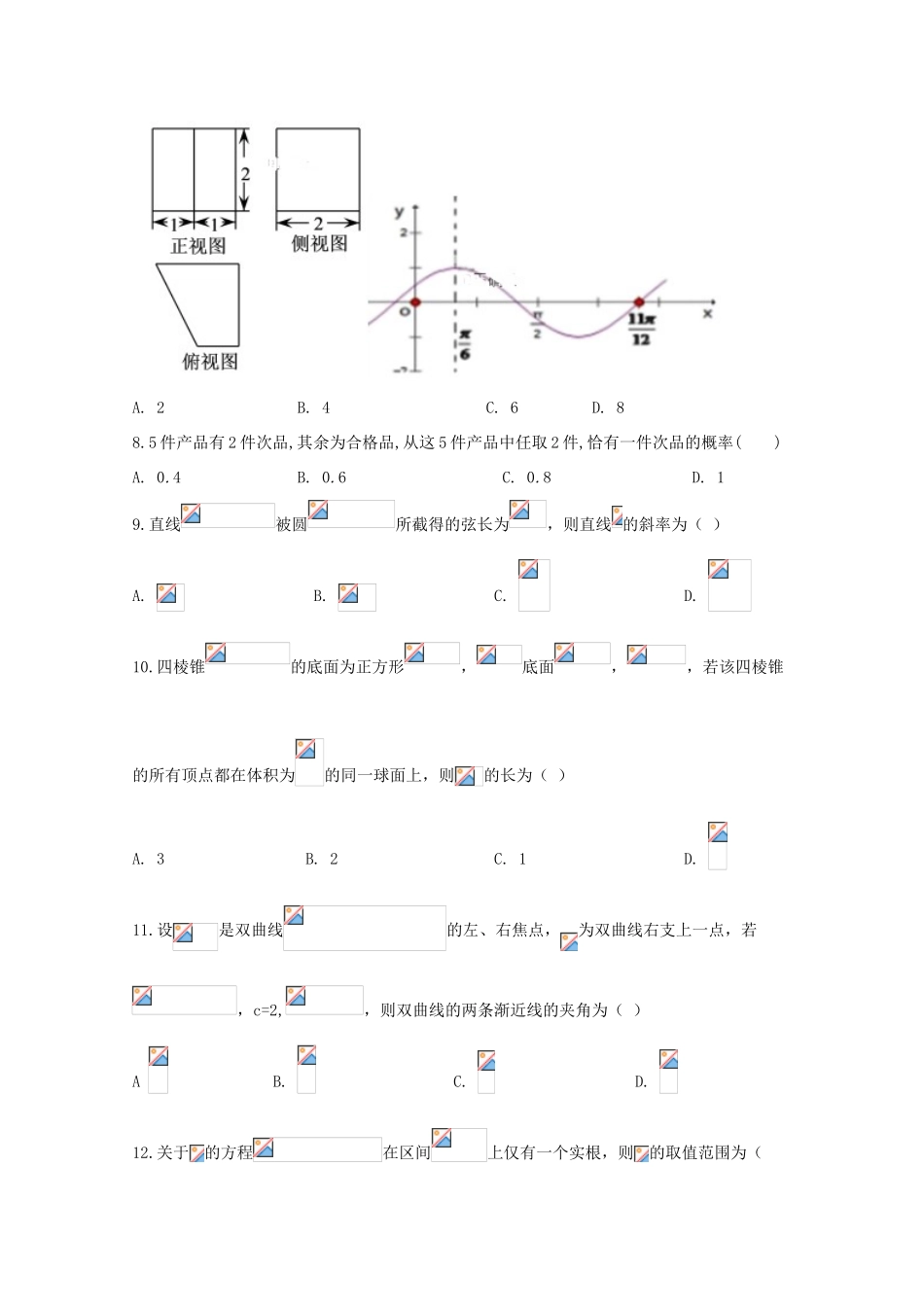
河南省鲁山县第一高级中学2021届高三数学上学期8月月考试题文一、选择题;(60分)1.已知集合,则()A.B.C.D.2.若:,,则()A.:,B.:,C.:,D.:,3.设向量,,,若与平行,则的值为()A.B.C.D.4.已知,则()A.B.C.D.5.已知,,则的大小关系为()A.B.C.D.6.已知等比数列中,若,且成等差数列,则()A.2B.2或32C.2或-32D.-17.某几何体三视图如图所示(单位:),则该几何体的体积(单位:)是()A.2B.4C.6D.88.5件产品有2件次品,其余为合格品,从这5件产品中任取2件,恰有一件次品的概率()A.0.4B.0.6C.0.8D.19.直线被圆所截得的弦长为,则直线的斜率为()A.B.C.D.10.四棱锥的底面为正方形,底面,,若该四棱锥的所有顶点都在体积为的同一球面上,则的长为()A.3B.2C.1D.11.设是双曲线的左、右焦点,为双曲线右支上一点,若,c=2,,则双曲线的两条渐近线的夹角为()AB.C.D.12.关于的方程在区间上仅有一个实根,则的取值范围为()A.B.C.D.二、填空题:(20分)13.函数的部分图象如左图所示,则将的图象向右平移个单位后,得到的图象对应的函数解析式为________.14.已知a>0,b>0,并且成等差数列,则的最小值为_________.15.已知f(x)是定义在R上的偶函数,且.若当时,,则__________16.,,,则的范围__________.三、解答题:(70分)17.(10)已知锐角三角形中,内角对边分别为,且(1)求角的大小。(2)求函数的值域。18.(12)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:平面BDE⊥平面PAC;(2)当PA∥平面BDE时,求三棱锥E-BCD的体积.19.(12)某市为调查统计高中男生身高情况,现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于和之间,将测量结果按如下方式分成6组:第1组,第2组,…,第6组,如图是按上述分组方法得到的频率分布直方图.(1)由频率分布直方图估计该校高三年级男生平均身高状况;(2)求这50名男生身高在以上(含)的人数.20.(12)已知椭圆C:的离心率,左、右焦点分别为,抛物线的焦点F恰好是该椭圆的一个顶点.(1)求椭圆C的方程;(2)已知圆M:的切线与椭圆相交于A、B两点,那么以AB为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由,21.(12)已知函数(1)当时,求函数单调区间;(2)若对任意,恒成立,求实数的取值范围.22.(12)直角坐标系xOy中,曲线C参数方程为(θ为参数),直线l的参数方程为.(1)若,求C与l的交点坐标;(2)若C上的点到l的距离的最大值为,求.文数答案一、选择题;1【答案】A2.【答案】A3.A4.【答案】D【详解】解:由=,可得,由,可得,故选D.5【详解】解:由于,,,可得,综合可得,故选B.6.已知等比数列中,若,且成等差数列,则()A.2B.2或32C.2或-32D.-1【答案】B【解析】【分析】根据等差数列与等比数列的通项公式及性质,列出方程可得q的值,可得的值.【详解】解:设等比数列的公比为q(),成等差数列,,,,解得:,,,故选B.7.【详解】解:由三视图可知该几何体为直四棱柱,其中底面为直角梯形,直角梯形的上底、下底分别为1cm、2cm,高为2cm,直四棱柱的高为2cm,可得直四棱柱的体积为,故选C.8【解析】件产品中有件次品,记为,,有件合格品,记为,,,从这件产品中任取件,有种,分别是,,,,,,,,,,恰有一件次品,有种,分别是,,,,,,设事件“恰有一件次品”,则,故选B.9.【详解】解:可得圆心(0,0)到直线的距离,由直线与圆相交可得,,可得d=1,即=1,可得,可得直线方程:,故斜率为,故选D.10.【详解】解:连接AC、BD交于点E,取PC的中点O,连接OE,可得OE∥PA,OE⊥底面ABCD,可得O到四棱锥的所有顶点的距离相等,即O为球心,设球半径为R,可得,可得,解得PA=1,故选C.11.【详解】解:由题意可得,可得,可得,可得a=1,,可得渐近线方程为:,可得双曲线的渐近线的夹角为,故选D.12.【详解】解:设,可得,令,可得,令,可得,可得函数递增区间为,递减区间为,由函数在区间上仅有一个零点,,,若,则,显然不符合题意,故,或,可得或,故选C.二、填空...