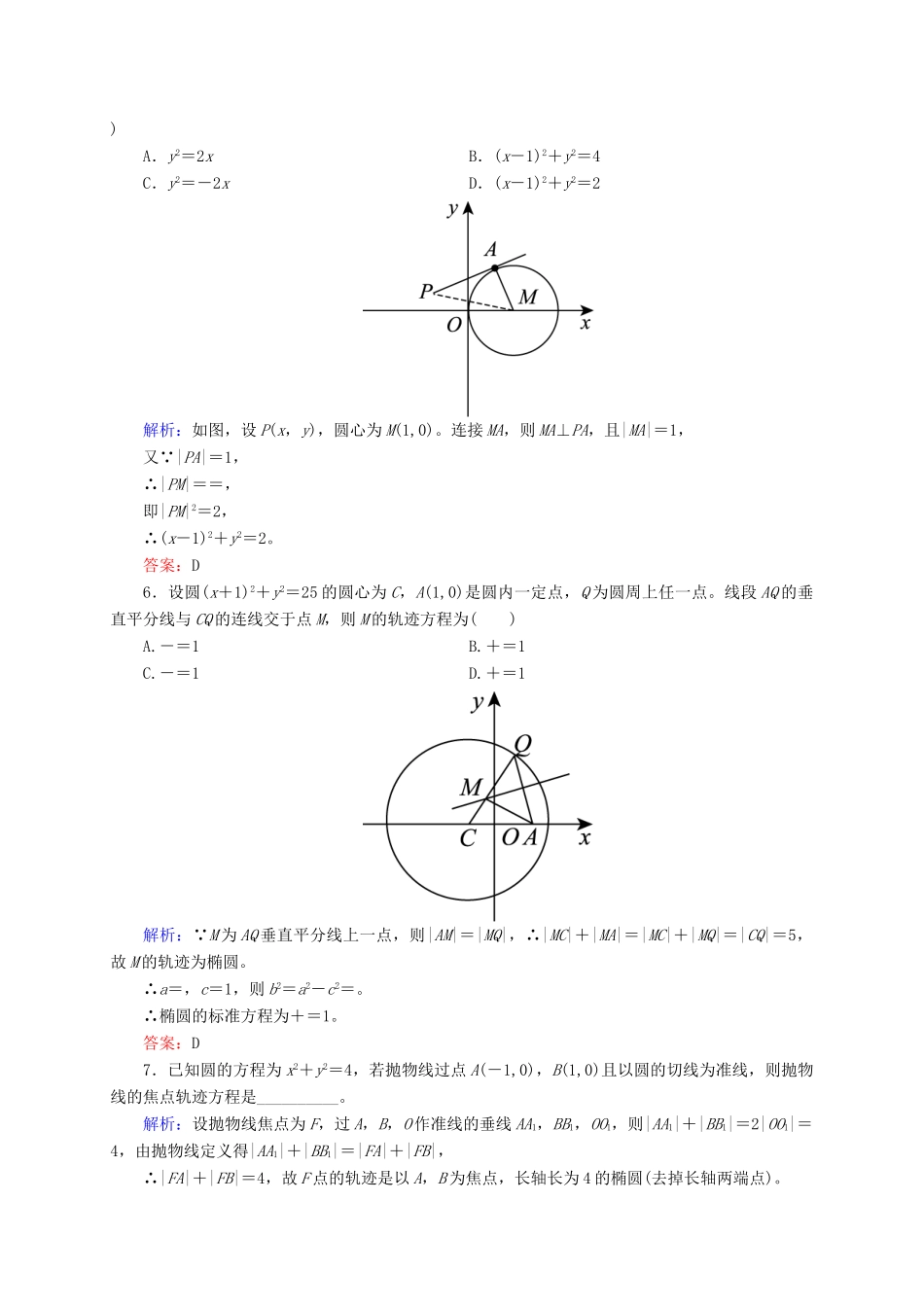
开卷速查(五十五)曲线与方程A级基础巩固练1.已知点F,直线l:x=-,点B是l上的动点。若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是()A.双曲线B.椭圆C.圆D.抛物线解析:由已知得|MF|=|MB|。由抛物线定义知,点M的轨迹是以F为焦点,l为准线的抛物线,故选D。答案:D2.如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是()A.椭圆B.双曲线C.抛物线D.圆解析:由条件知|PM|=|PF|。∴|PO|+|PF|=|PO|+|PM|=|OM|=R>|OF|。∴P点的轨迹是以O,F为焦点的椭圆。答案:A3.已知点A(1,0),直线l:y=2x-4,点R是直线l上的一点,若RA=AP,则点P的轨迹方程为()A.y=-2xB.y=2xC.y=2x-8D.y=2x+4解析:设P(x,y),R(x1,y1),由RA=AP知,点A是线段RP的中点,∴即 点R(x1,y1)在直线y=2x-4上,∴y1=2x1-4,∴-y=2(2-x)-4,即y=2x。答案:B4.已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则Q点的轨迹方程是()A.2x+y+1=0B.2x-y-5=0C.2x-y-1=0D.2x-y+5=0解析:设Q(x,y),则P为(-2-x,4-y),代入2x-y+3=0得2x-y+5=0。答案:D5.设点A为圆(x-1)2+y2=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为()A.y2=2xB.(x-1)2+y2=4C.y2=-2xD.(x-1)2+y2=2解析:如图,设P(x,y),圆心为M(1,0)。连接MA,则MA⊥PA,且|MA|=1,又 |PA|=1,∴|PM|==,即|PM|2=2,∴(x-1)2+y2=2。答案:D6.设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点。线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为()A.-=1B.+=1C.-=1D.+=1解析: M为AQ垂直平分线上一点,则|AM|=|MQ|,∴|MC|+|MA|=|MC|+|MQ|=|CQ|=5,故M的轨迹为椭圆。∴a=,c=1,则b2=a2-c2=。∴椭圆的标准方程为+=1。答案:D7.已知圆的方程为x2+y2=4,若抛物线过点A(-1,0),B(1,0)且以圆的切线为准线,则抛物线的焦点轨迹方程是__________。解析:设抛物线焦点为F,过A,B,O作准线的垂线AA1,BB1,OO1,则|AA1|+|BB1|=2|OO1|=4,由抛物线定义得|AA1|+|BB1|=|FA|+|FB|,∴|FA|+|FB|=4,故F点的轨迹是以A,B为焦点,长轴长为4的椭圆(去掉长轴两端点)。答案:+=1(y≠0)8.△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是__________。解析:如图,|AD|=|AE|=8,|BF|=|BE|=2,|CD|=|CF|,所以|CA|-|CB|=8-2=6。根据双曲线定义,所求轨迹是以A,B为焦点,实轴长为6的双曲线的右支,方程为-=1(x>3)。答案:-=1(x>3)9.动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则动点P的轨迹方程为__________。解析:由抛物线定义知点P的轨迹是以F(2,0)为焦点的抛物线,设抛物线的方程为y2=2px,从而可知p=4,所以动点P的轨迹方程为y2=8x。答案:y2=8x10.已知椭圆的中心是坐标原点O,焦点F1,F2在y轴上,它的一个顶点为A(,0),且中心O到直线AF1的距离为焦距的,过点M(2,0)的直线l与椭圆交于不同的两点P,Q,点N在线段PQ上。(1)求椭圆的标准方程;(2)设|PM|·|NQ|=|PN|·|MQ|,求动点N的轨迹方程。解析:(1)设椭圆的标准方程是+=1(a>b>0)。由于椭圆的一个顶点是A(,0),故b2=2。根据题意得∠AF1O=,sin∠AF1O=,即a=2b,a2=8,所以椭圆的标准方程是+=1。(2)设P(x1,y1),Q(x2,y2),N(x,y),由题意知,直线l的斜率存在,设直线l的方程为y=k(x-2)。直线l的方程与椭圆方程联立消去y得(k2+4)x2-4k2x+4k2-8=0。由Δ=16k4-4(k2+4)(4k2-8)>0,得-2<k<2。根据根与系数的关系得x1+x2=,x1x2=。又|PM|·|NQ|=|PN|·|MQ|,即(2-x1)(x2-x)=(x-x1)(2-x2)。解得x=1,代入直线l的方程得y=-k,y∈(-2,2)。所以动点N的轨迹方程为x=1,y∈(-2,2)。B级能力提升练11.设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP0,垂足为P0,且MP0=PP0。(1)求点M的轨迹C...