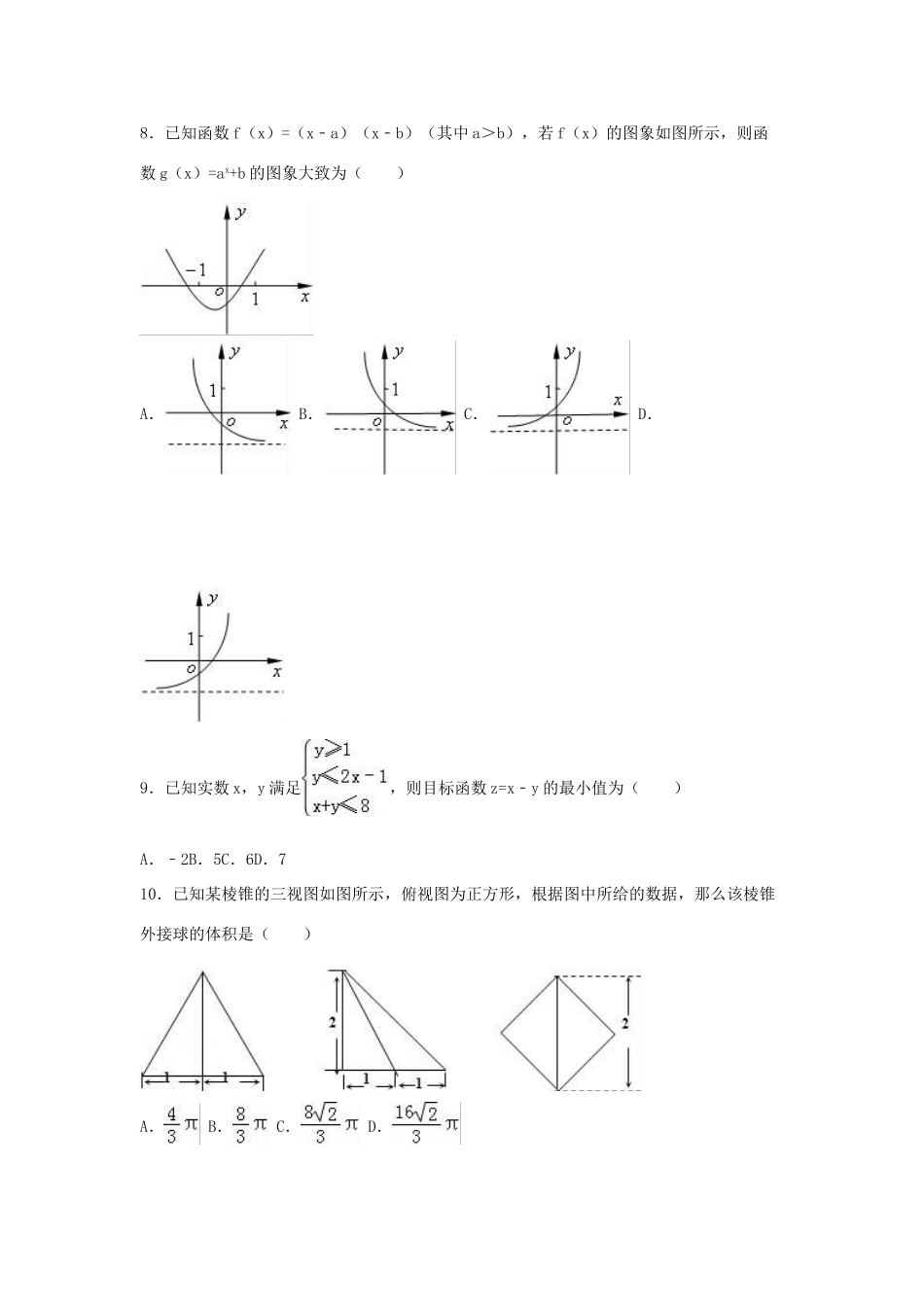
2016年宁夏石嘴山市平罗中学高考数学一模试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|1≤x≤2},B={x|x2﹣1≤0},则A∩B=()A.{x|﹣1<x<1}B.{x|﹣1<x<2}C.{1}D.∅2.复数(i是虚数单位)的虚部为()A.﹣2B.﹣1C.1D.23.在下列函数中既是奇函数,又是在区间(0,+∞)上单调递减的函数为()A.B.y=x﹣1C.D.y=x3+x4.如图所示的程序框图,其作用是输入x的值,输出相应的y值,若输入,则输出的y值为()A.2B.C.2﹣2πD.85.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.116.在△ABC,a=,b=,B=,则A等于()A.B.C.D.或7.“x<1”是“”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件8.已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为()A.B.C.D.9.已知实数x,y满足,则目标函数z=x﹣y的最小值为()A.﹣2B.5C.6D.710.已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据,那么该棱锥外接球的体积是()A.B.C.D.11.已知函数的图象上相邻两个最高点的距离为π,若将函数f(x)的图象向左平移个单位长度后,所得图象关于y轴对称.则f(x)的解析式为()A.f(x)=2sin(x+)B.f(x)=2sin(x+)C.f(x)=2sin(2x+)D.f(x)=2sin(2x+)12.如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为,则圆锥底面圆的半径等于()A.1mB.C.D.2m二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中对应题号后的横线上.13.已知向量=(1,x),=(x﹣1,2),若,则x=.14.设=2,则tan(α+)=.15.已知函数f(x)=,则f已知双曲线﹣=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为.三、解答题:本大题共5小题,满分60分.解答须写出文字说明,证明过程和演算步骤.17.已知等差数列{an}满足a1+a3=8,a2+a4=12.(Ⅰ)求数列{an}的前n项和为Sn;(Ⅱ)若++…+=,求n的值.18.某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.(1)求100名玩家中各年龄组的人数,并利用所给的频率分布直方图估计该款游戏所有玩家的平均年龄;(2)若已从年龄在[35,45),[45,55)的玩家中利用分层抽样选取6人组成一个游戏联盟,现从这6人中选出2人,求这两人在不同年龄组的概率.19.如图,在正三棱柱ABC﹣A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.(1)若M、N分别是CC1、AB的中点,求证:CN∥平面AB1M;(2)求证:不论M在何位置,三棱锥A1﹣AMB1的体积都为定值,并求出该定值.20.已知椭圆的左,右焦点分别为F1,F2,离心率为,且经过点.(1)求椭圆C的方程;(2)直线l:y=x+m与椭圆C相切,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,求四边形F1MNF2的面积.21.已知函数f(x)=(ax﹣2)ex在x=1处取得极值.(Ⅰ)求a的值;(Ⅱ)求函数f(x)在[m,m+1]上的最小值;(Ⅲ)求证:对任意x1,x2∈[0,2],都有|f(x1)﹣f(x2)|≤e.[选修4-1:几何证明选讲]22.如图,A,B,C为⊙O上的三个点,AD是∠BAC的平分线,交⊙O于点D,过B作⊙O的切线交AD的延长线于点E.(Ⅰ)证明:BD平分∠EBC;(Ⅱ)证明:AE•DC=AB•BE.[选修4-4:坐标系与参数方程]23.在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ﹣2sinθ,直线l的极坐标方程为2aρcosθ+2ρsinθ=1(a为常数).(1)求直线l与圆C的普通方程;(2)若直线l分圆C所得两弧长度之比为1:2,求实数a的值.[选修4-5:不等式选讲]24.已知函数f(x)=log2(|x+1|+|x﹣2|﹣m).(1)当m=7时,求函数f(x)的定义域;(2)若关于x的不等式f(x)≥2的解集是R,求m...