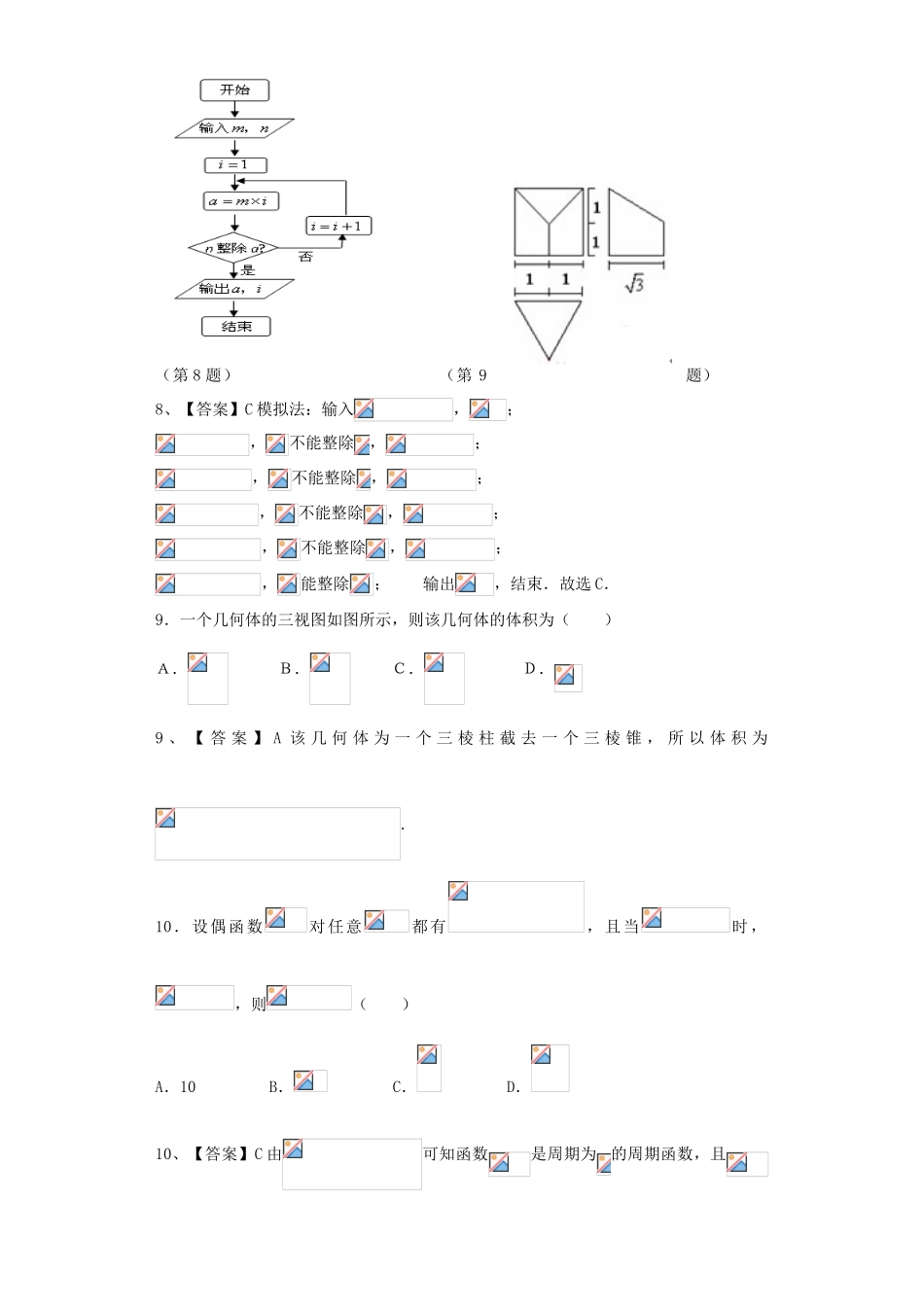
武鸣高中2016届高三8月月考数学(文)试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A.B.C.D.1、【答案】C2.命题“∀,||”的否定是()A.∀,||B.∀,||C.∃,||D.∃,||2、【答案】C根据全称命题的否定形式,可知应该为,||,故选C3.已知平面向量,且,则()A.B.C.D.3、【答案】B,4.函数的定义域为()A.B.C.D.4、【答案】A因为,所以定义域为.5.△ABC中,BC=2,B=,当△ABC的面积等于时,sinC的值为()A.B.C.D.5、【答案】B,代入面积公式,,所以,又根据余弦定理,,所以,根据正弦定理,,代入数据:,解得6.使命题“对任意的∈[1,2],2-≤0”为真命题的一个充分不必要条件是()A.≥4B.≤4C.≥5D.≤56、【答案】C当“对任意的,”为真命题时,即在上恒成立.因为,所以可得.由题意分析可知C正确.7.在△ABC中,角A,B,C所对的边分别是a,b,c,若acosB=bcosA,则△ABC是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形7、【答案】A根据正弦定理,边化角,得到,整理为,得到,即是等腰三角形.8.右边程序框图中,若输入,,则输出的值别是()A.B.C.D.(第8题)(第9题)8、【答案】C模拟法:输入,;,不能整除,;,不能整除,;,不能整除,;,不能整除,;,能整除;输出,结束.故选C.9.一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.9、【答案】A该几何体为一个三棱柱截去一个三棱锥,所以体积为.10.设偶函数对任意都有,且当时,,则()A.10B.C.D.10、【答案】C由可知函数是周期为的周期函数,且是偶函数,所以11、已知三棱锥的底面是以为斜边的等腰直角三角形,,则三棱锥的外接球的球心到平面的距离是()A.B.1C.D.11、【答案】A三棱锥的底面是以为斜边的等腰直角三角形,,在面内的射影为中点,平面,上任意一点到的距离相等。,在面内作的垂直平分线,则为的外接球球心。,,即为到平面的距离。故选A。12.直线过抛物线的焦点,且交抛物线于两点,交其准线于点,已知,则()A.2B.C.D.412、【答案】C过A,B分别作准线的垂线交准线于E,D.因为,所以,且,设,则,根据三角形的相似性可得,即,解得,所以,即,所以,选C..二、填空题:本大题共4小题,每小题5分,共20分.13.若变量满足约束条件:,则的最大值为.13【答案】4约束条件为一个三角形ABC及其内部,其中,因此直线过点时取最大值4.14、设是实数,若复数(为虚数单位)在复平面内对应的点在直线上,则的值为.14、【答案】a=0由复数可化为.复数对应的点在直线上,所以可得.15.若函数对任意的恒成立,则.15、【答案】:因为,所以函数为单调递增的奇函数,因此即16、我们把离心率的双曲线称为黄金双曲线.如图是双曲线的图象,给出以下几个说法:①双曲线是黄金双曲线;②若,则该双曲线是黄金双曲线;③若为左右焦点,为左右顶点,(0,),(0,﹣)且,则该双曲线是黄金双曲线;④若经过右焦点且,,则该双曲线是黄金双曲线.其中正确命题的序号为.16、【答案】①②③④对于①,,则,,,所以双曲线是黄金双曲线;对于②,,整理得解得,所以双曲线是黄金双曲线;三、解答题:解答应写出文字说明.证明过程或演算步骤17(本小题满分12分)已知是等差数列,满足,数列满足,且为等比数列.(1)求数列的通项公式;(2)求数列的前n项和.17、解析:(1)设等差数列{an}的公差为d,由题意得d===3.所以an=a1+(n-1)d=3n(n=1,2,…).设等比数列{bn-an}的公比为q,由题意得q3===8,解得q=2.所以bn-an=(b1-a1)qn-1=2n-1.从而bn=3n+2n-1(n=1,2,…).(2)由(1)知bn=3n+2n-1(n=1,2,…).数列{3n}的前n项和为n(n+1),数列{2n-1}的前n项和为=2-1.所以,数列{bn}的前n项和为n(n+1)+2-1.18.(本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组,第二组,,第五组.右图是按上述分组方法得到的频率分布直方图.按上述分...