高三数学1月月考试题-人教版高三全册数学试题VIP免费

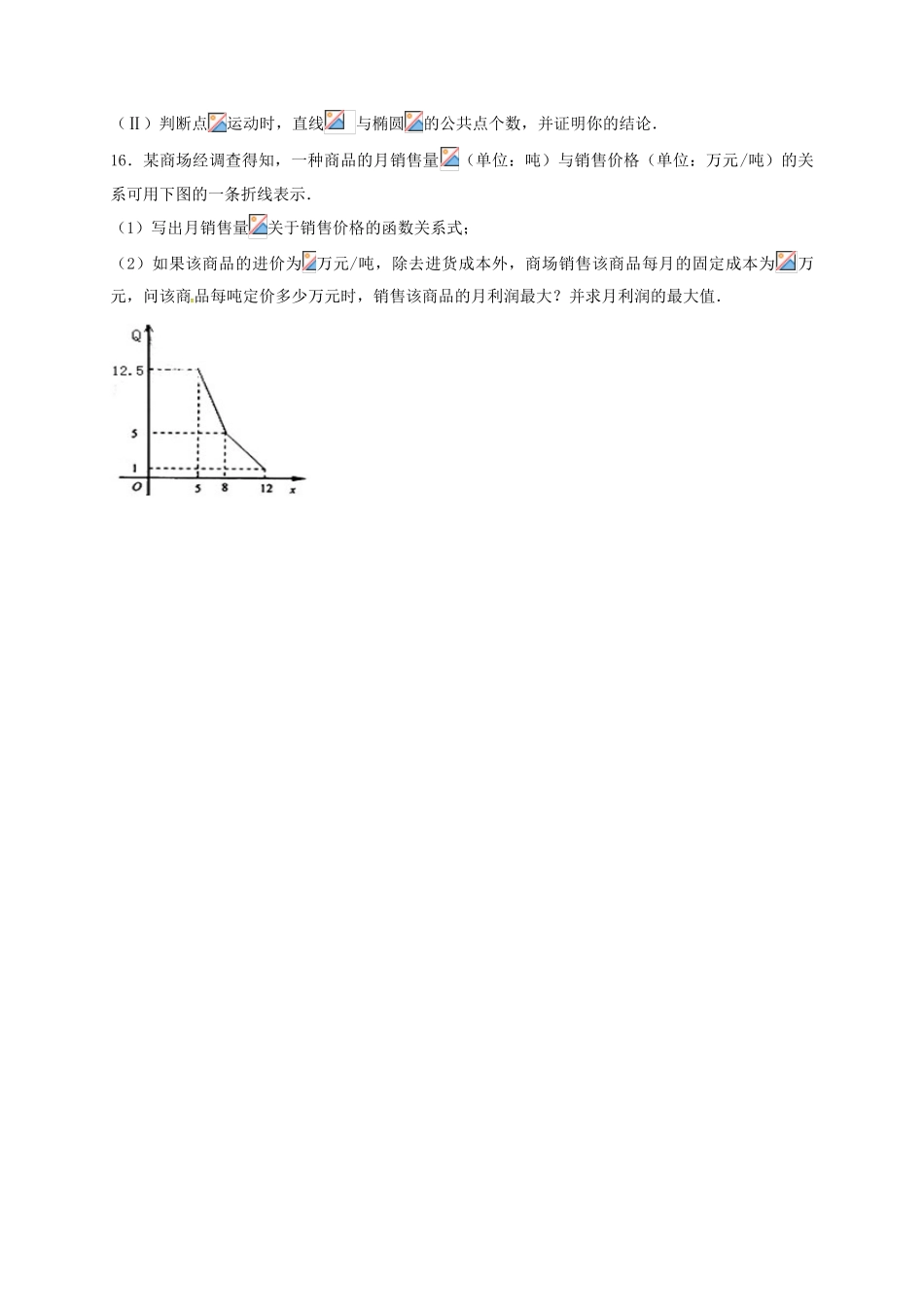
2015-2016学年度上学期高三数学1月月考卷一、选择题1．如果导函数图像的顶点坐标为，那么曲线上任一点的切线的倾斜角的取值范围是（）A．B．C．D．2．（2015•山东模拟）已知实数1，m，9成等比数列，则圆锥曲线=1的离心率为（）A．B．2C．或2D．或3．[2012·湖南高考]函数f(x)＝sinx－cos(x＋)的值域为()A.[－2,2]B.[－，]C.[－1,1]D.[－，]4．过点（1，0）且与直线x-2y-2=0平行的直线方程是（）A．x-2y-1=0B．x-2y+1=0C．2x+y-2=0D．x+2y-1=05．已知向量，，，且，则实数＝（）A．B．C．3D．06．一个单位有职工160人，其中有业务员104人，管理人员32人，后勤服务人员24人，要从中抽取一个容量为20的样本，用分层抽样的方法抽取样本，则在20人的样本中应抽取管理人员人数为（）A．3B．4C．5D．67．（2012•河北模拟）已知直线y=kx是y=lnx的切线，则k的值是（）A.eB.﹣eC.D.﹣8．将两个顶点在抛物线y2＝2px(p＞0)上，另一个顶点是此抛物线焦点的正三角形个数记为n，则()A．n＝0B．n＝1C．n＝2D．n≥39．如图，椭圆的中心在坐标原点，焦点在轴上，为椭圆顶点，为右焦点，延长与交于点，若为钝角，则该椭圆离心率的取值范围是（）第3题图ODGCAEFBPA．B．C．D．10．已知二面角的大小为，为空间中任意一点，则过点且与平面和平面所成的角都是的直线的条数为（）A．1B．2C．3D．4二、填空题11．设，若，则12．已知函数f(x)的自变量取值区间为，若其值域也为，则称区间为的保值区间．若的保值区间是[2，＋∞)，则的值为________．13．设点P是曲线y＝x2上的一个动点，曲线y＝x2在点P处的切线为l，过点P且与直线l垂直的直线与曲线y＝x2的另一交点为Q，则PQ的最小值为________．三、解答题14．如图,是以为直径的上一点,于点,过点作的切线,与的延长线相交于点是的中点,连结并延长与相交于点,延长与的延长线相交于点.(1)求证:；(2)求证:是的切线；(3)若,且的半径长为,求和的长度.15．（本小题满分12分）已知椭圆的左右焦点分别是，直线的方程是，点是椭圆上动点（不在轴上），过点作直线的垂线交直线于点，当垂直轴时，点的坐标是．（Ⅰ）求椭圆的方程；（Ⅱ）判断点运动时，直线与椭圆的公共点个数，并证明你的结论．16．某商场经调查得知，一种商品的月销售量（单位：吨）与销售价格（单位：万元/吨）的关系可用下图的一条折线表示．（1）写出月销售量关于销售价格的函数关系式；（2）如果该商品的进价为万元/吨，除去进货成本外，商场销售该商品每月的固定成本为万元，问该商品每吨定价多少万元时，销售该商品的月利润最大？并求月利润的最大值．参考答案1．D试题分析：的导数为，因为其图像的顶点坐标为，所以图象开口向上，最小值为-，即，任一点的切线的倾斜角的取值范围是，选D。考点：本题主要考查导数的几何意义，直线的倾斜角，二次函数的图象和性质，正切函数的性质。点评：小综合题，曲线在某点的导数，就是过该点的切线的斜率。2．C试题分析：由1，m，9构成一个等比数列，得到m=±3．当m=3时，圆锥曲线是椭圆；当m=﹣3时，圆锥曲线是双曲线，由此即可求出离心率．解： 1，m，9构成一个等比数列，∴m2=1×9，则m=±3．当m=3时，圆锥曲线+y2=1是椭圆，它的离心率是=；当m=﹣3时，圆锥曲线+y2=1是双曲线，它的离心率是=2．则离心率为或2．故选C．考点：双曲线的简单性质；椭圆的简单性质．3．B因为f(x)＝sinx－cosx＋sinx＝(sinx－cosx)＝sin(x－)，所以函数f(x)的值域为[－，]．4．A试题分析：设与直线平行的直线方程为，将点代入直线方程可得，解得．则所求直线方程为．故A正确．考点：两直线平行．【方法点睛】本题主要考查两直线的平行问题，属容易题．两直线平行倾斜角相等，所以斜率相等或均不存在．所以与直线平行的直线方程可设为．5．C试题分析： ，，∴， ，且，∴，即．考点：向量的运算．6．B试题分析：求出每个个体被抽到的概率，用该层的个体数乘以每个个体被抽到的概率，就等于该层应抽取的个体数．解：每个个体被抽到的概率等于=，32×=4，故选B．考点：分层抽样方法．7．C试题分析：欲求k的值，只须求出切线的斜率的值即可，故先利用导数求出在切处的导函数值，...