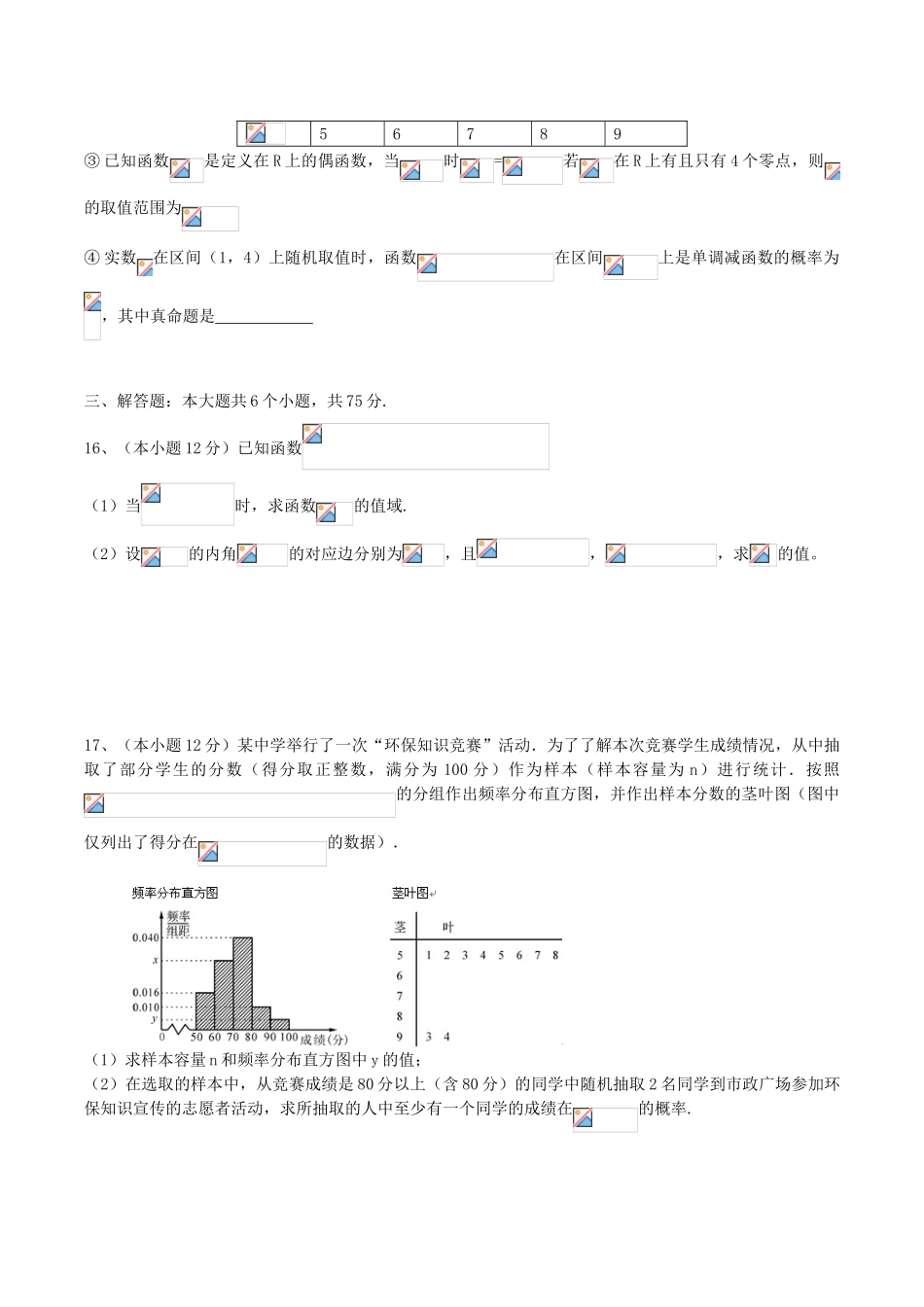
眉山中学2016届1月月考数学(文史类)一、选择题:本大题共10个小题,每小题5分,共50分.在给出的四个选项中,只有一个是符合题目要求1、已知集合集合则()A.B.C.D.2、为虚数单位,若,则()A.1B.C.D.23、下列有关命题的说法正确的是()A.命题“”的否定是:“”B.“”是“”的充要条件C.命题:“若则”的逆否命题为真命题D.数据1,3,2,4,3,5的平均数、众数、中位数都是34、对于不重合的两个平面和,给定下列条件:①存在直线,使得且;②存在平面,使得且;③内有不共线三点到平面的距离相等;④存在异面直线,,使得,,,。其中可以判定与平行的条件有()A.1个B.2个C.3个D.4个5、数列中,,向量(其中),若向量,则数列的通项公式是()A.B.C.D.6、一算法的程序框图如右图,若输出的则输入的的值可能为()A.9B.3C.0D.-67、过双曲线的右顶点作轴的垂线与的一条渐近线交于点,若以的右焦点为圆心、半径为2的圆经过、两点(为坐标原点),则双曲线的方程为()A.B.C.D.8、已知函数若且则的取值范围是()A.B.C.D.9、函数的部分图象如图所示,如果,且,则()A.B.C.D.110、已知函数,若方程有两个零点,则实数的取值范围是()A.B.C.D.二、填空题(共5小题,每小题5分,共25分)11.求值12.设变量满足,则目标函数的最小值为13.已知,则14.设曲线在点(1,1)处的切线与轴的交点的横坐标为,令,则15、给出下列命题①若奇函数对定义域R内任意都有则为周期函数②根据表中数据,可以判定方程的一个根所在的区间为(1,2)-101230.3712.727.3920.0956789③已知函数是定义在R上的偶函数,当时=若在R上有且只有4个零点,则的取值范围为④实数在区间(1,4)上随机取值时,函数在区间上是单调减函数的概率为,其中真命题是三、解答题:本大题共6个小题,共75分.16、(本小题12分)已知函数(1)当时,求函数的值域.(2)设的内角的对应边分别为,且,,求的值。17、(本小题12分)某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在的数据).(1)求样本容量n和频率分布直方图中y的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的人中至少有一个同学的成绩在的概率.18、(本小题12分)如图,三角形是边长为4的正三角形,底面,,点是的中点,点在上,且.(1)证明:平面平面;(2)求三棱锥的体积19、(本小题12分)数列中,当时,其前项和为,满足(1)求证:数列是等差数列,并求的表达式;(2)设数列的前项和为,不等式对所有的恒成立,求正整数的最大值.20、(本小题13分)已知椭圆的中心在坐标原点,其焦点与双曲线:的焦点重合,且椭圆的短轴的两个端点与其一个焦点构成正三角形.(1)求椭圆的方程;(2)过双曲线的右顶点作直线与椭圆交于不同的两点、。设点(4,3),记直线、的斜率分别为,求证:为定值,求出此定值.21、(本小题14分)已知函数(1)当时,求函数在处的切线方程(2)在(1)的前提下,若函数的图象恒不在曲线的下方,求k的取值范围(3)若在定义域上是单调函数,且零点为1,求的取值范围