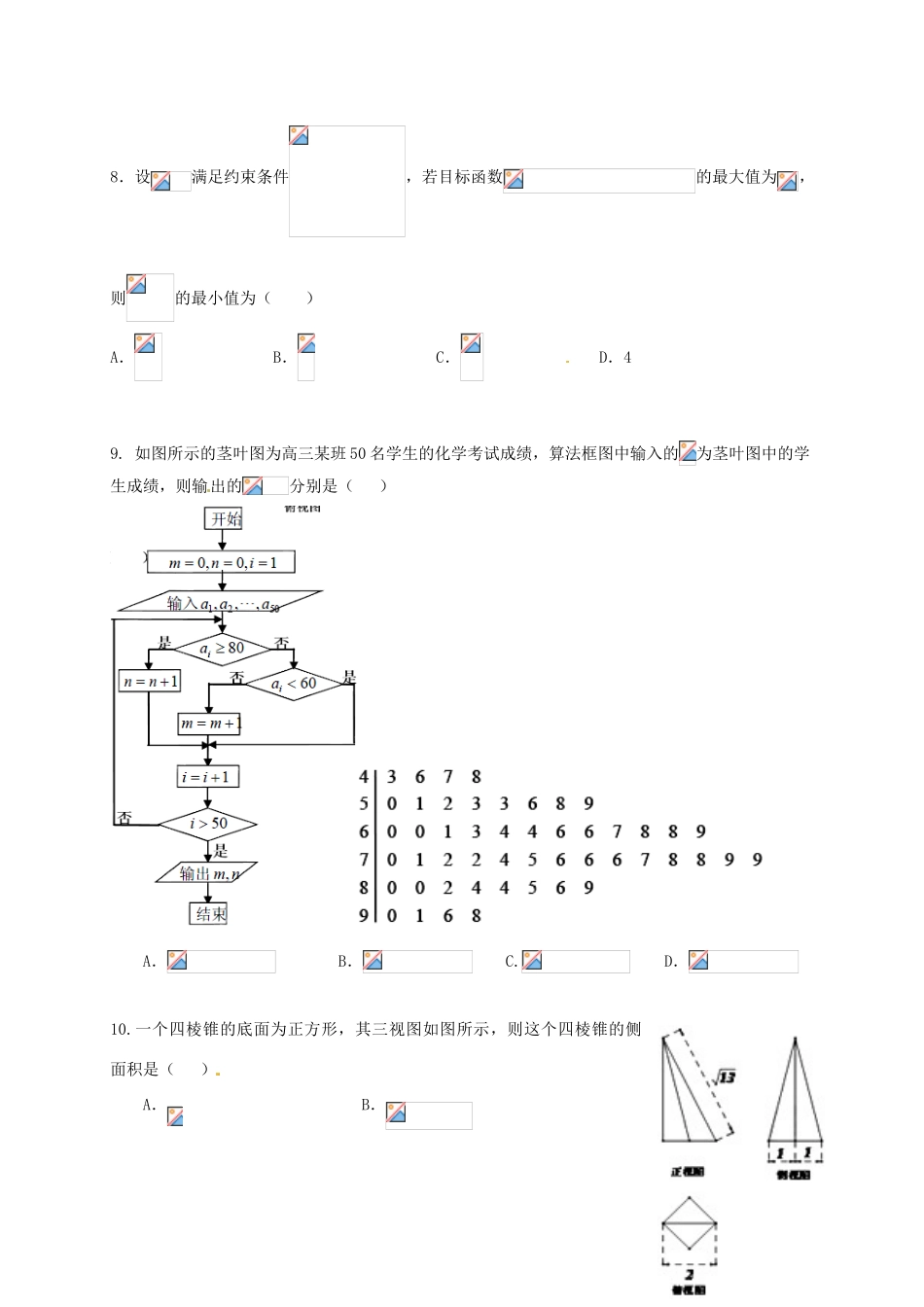
成都外国语学校高2014级一诊模拟数学(文史类)一、选择题:1.已知集合A=,B=,则AB=()A.B.C.D.2.复数的共轭复数是()A.B.C.D.3.给出下列关于互不相同的直线、、和平面、的四个命题:①若,,点,则与不共面;②若、是异面直线,,,且,,则;③若,,,则;④若,,,,,则,其中为真命题的是()A.①③④B.②③④C.①②④D.①②③4.已知数列为等差数列,若,则的值为()A.B.C.D.5.设O是△ABC的外心(三角形外接圆的圆心).若,则∠BAC的度数等于()A.30°B.45°C.60°D.90°6.若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是()A.多于4个B.4个C.3个D.2个7.已知函数f(x)=sin(2x+α)在x=时有极大值,且f(x-β)为奇函数,则α,β的一组可能值依次为()A.,-B.,C.,-D.,8.设满足约束条件,若目标函数的最大值为,则的最小值为()A.B.C.D.49.如图所示的茎叶图为高三某班50名学生的化学考试成绩,算法框图中输入的为茎叶图中的学生成绩,则输出的分别是()A.B.C.D.10.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是()A.B.C.D.11.已知双曲线的右焦点为,设,为双曲线上关于原点对称的两点,的中点为,的中点为,若原点在以线段为直径的圆上,直线的斜率为,则双曲线的离心率为()A.4B.2C.D.12.已知定义在R上的奇函数,满足恒成立,且,则下列结论正确的是()A.B.C.D.二、填空题:13.过点作圆的两条切线,设切点分别为,则线段的长度为14.如图,为测量山高,选择和另一座山的山顶为测量观测点.从点测得点的俯角,点的仰角以及;从点测得已知山高,则山高.15.已知函数,若是从三个数中任取的一个数,是从三个数中任取的一个数,则使函数有极值点的概率为_______.16.已知,方程有四个不同的解,且,则的取值范围为.三、解答题:17.(本题满分12分)设数列的前项和满足:,等比数列的前项和为,公比为,且.(I)求数列的通项公式;(II)求数列的前项和为.18.(12分)微信是现代生活进行信息交流的重要工具,据统计,某公司名员工中的人使用微信,其中每天使用微信时间在一小时以内的有人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于岁)和中年(年龄不小于岁)两个阶段,使用微信的人中是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中是青年人.(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出列联表;青年人中年人合计经常使用微信不经常使用微信合计(Ⅱ)由列联表中所得数据,是否有的把握认为“经常使用微信与年龄有关”?(Ⅲ)采用分层抽样的方法从“经常使用微信”的人中抽取人,从这人中任选人,求事件“选出的人均是青年人”的概率.附:19.如图,在四棱锥中,底面,底面是矩形,,是的中点.(1)求证:平面平面;(2)已知点是的中点,点是上一点,且平面平面.若,求点到平面的距离.20.(本小题满分12分)已知动圆与圆相切,且与圆相内切,记圆心的轨迹为曲线;设为曲线上的一个不在轴上的动点,为坐标原点,过点作的平行线交曲线于两个不同的点.(1)求曲线的方程;(2)试探究和的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;(3)记的面积为,的面积为,令,求的最大值.21.(本小题满分12分)已知函数.(I)求的单调区间和极值;(II)设,且,证明:.选做题22.已知直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为.(I)求圆的直角坐标方程;(II)若是直线与圆面的公共点,求的取值范围.23.设函数.(I)若不等式的解集为,求的值;(II)若存在,使,求的取值范围.成都外国语学校高2017届一诊模拟试题文科数学四、选择题:1.A2.C【解析】因为,所以共轭复数是,选C.考点:共轭复数3.C4.A5.C【解析】:选C取BC的中点D,连接AD,则+=2.由题意得3=2,∴AD为BC的中线且O为重心.又O为外心,∴△ABC为正三角形,∴∠BAC=60°.6.7.D【解析】:选D.依题意得2×+α=2...