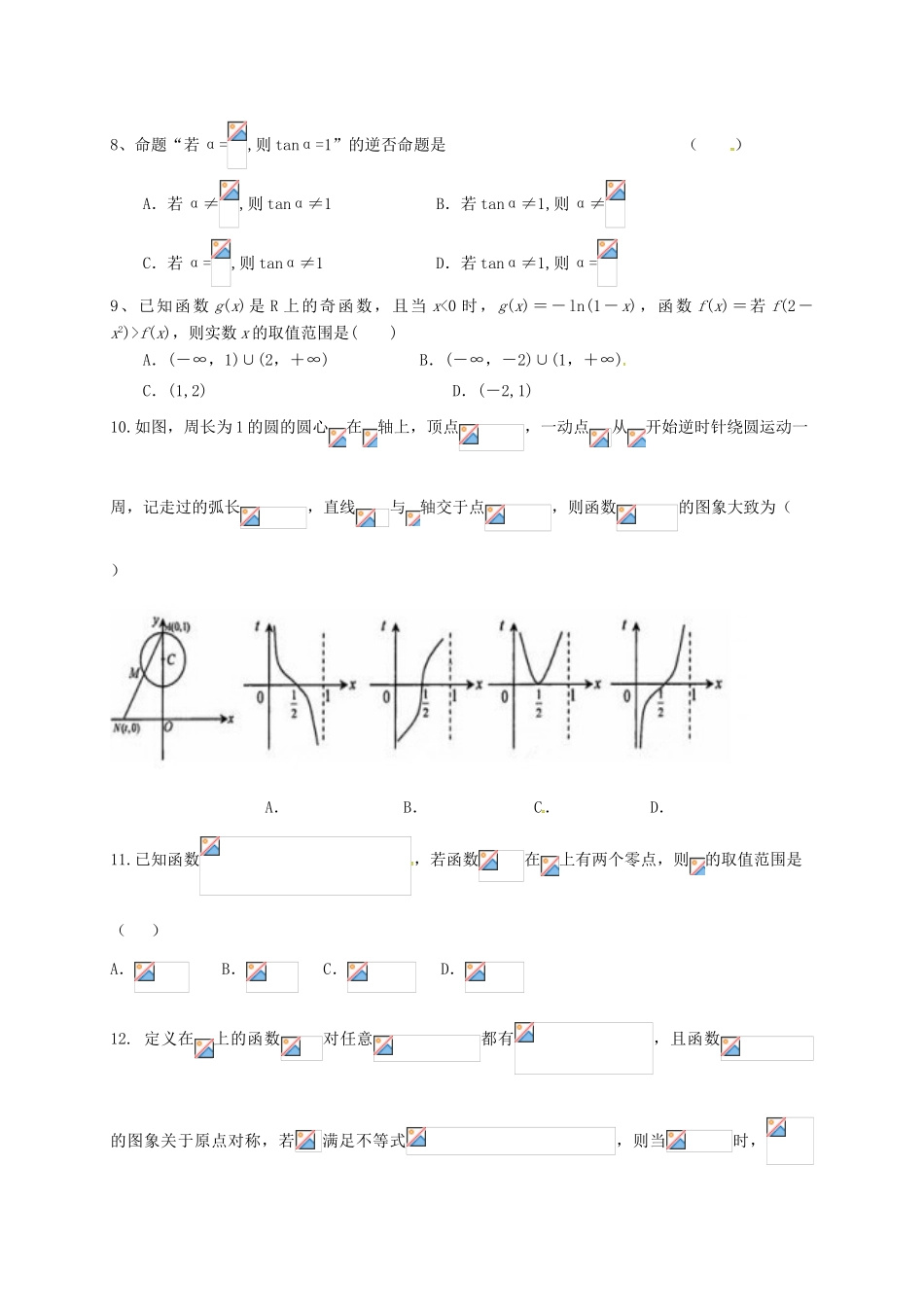
周口中英文学校2016—2017学年度上期十月考试高三数学试题时间:120分钟满分:150分一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则()A.B.C.D.2.设,则“”是“直线与直线平行”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.下列函数中,在其定义域内既是偶函数又在(-∞,0)上单调递增的函数是()A.f(x)=x2B.f(x)=2|x|C.f(x)=log2D.f(x)=sinx4.已知函数的图象是连续不断的,有如下的的对应表则函数存在零点的区间有()A.区间和B.区间、和C、区间和D.区间、和5、定义在上的函数满足时,,则的值为()A.8B.0C.2D.-26、y=-log2(4-x2)的定义域是()A.(-2,0)∪(1,2)B.(-2,0]∪(1,2)C.(-2,0)∪[1,2)D.[-2,0]∪[1,2]7、已知f(x)=是(-∞,+∞)上的减函数,那么a的取值范围是()A.(0,1)B.C.D.8、命题“若α=,则tanα=1”的逆否命题是()A.若α≠,则tanα≠1B.若tanα≠1,则α≠C.若α=,则tanα≠1D.若tanα≠1,则α=9、已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),函数f(x)=若f(2-x2)>f(x),则实数x的取值范围是()A.(-∞,1)∪(2,+∞)B.(-∞,-2)∪(1,+∞)C.(1,2)D.(-2,1)10.如图,周长为1的圆的圆心在轴上,顶点,一动点从开始逆时针绕圆运动一周,记走过的弧长,直线与轴交于点,则函数的图象大致为()A.B.C.D.11.已知函数,若函数在上有两个零点,则的取值范围是()A.B.C.D.12.定义在上的函数对任意都有,且函数的图象关于原点对称,若满足不等式,则当时,的取值范围是()A.B.C.D.二、(本题有4个小题,每题5分,共20分)13、命题“对任意的x<0,x3-x2+1≤0”的否定是14.定义运算法则如下:;若,则M+N=;15、函数的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则+的最小值为16.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数称为狄利克雷函数,则关于函数有以下四个命题:①;②函数是偶函数;③任意一个非零有理数,对任意恒成立;④存在三个点,,,使得为等边三角形.其中真命题的序号三.解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分为12分)已知命题p:x∈[1,2],x2-a≥0;命题q:x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。18、(本小题满分为12分)已知函数是上的奇函数,且的图象关于对称,当时,.(1)当时,求的解析式;(2)计算的值.19.(本大题12分)已知二次函数.(1)判断命题:“对于任意的R(R为实数集),方程必有实数根”的真假,并写出判断过程(2),若在区间及内各有一个零点.求实数a的范围20、(本小题满分12分)已知定义在区间上的两个函数和,其中,,(Ⅰ)求函数的最小值;(Ⅱ)对于,恒成立,求实数的取值范围.20、(本小题满分12分)已知函数满足,对于任意R都有,且,令.(1)求函数的表达式;(2)求函数的单调区间;(3)研究函数在区间上的零点个数.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号22.(本小题满分10分)选修4-4:极坐标系与参数方程已知曲线的参数方程为(为参数),以直角坐标系原点为极点,轴正半轴为极轴建立极坐标系.(Ⅰ)求曲线的极坐标方程;(Ⅱ)若直线的极坐标方程为,求直线被曲线截得的弦长.23.(本小题满分10分)选修4-5:不等式选讲已知函数,不等式的解集为.(Ⅰ)求实数的值;(Ⅱ)若对一切实数恒成立,求实数的取值范围.周口中英文学校2016—2017学年度上期十月考试高三数学试题答案一、选择题二、填空题:(本题有4个小题,每题5分,共20分)13、“存在x<0,x3-x2+1>0”14、515、816、①②③④三.解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)解:p真,则---------2分q真,则即----------4分“”为真,为假中必有一个为真,另一个为假----5分当时,有-------8分当时,有--------11分实数a的取值范围为.--------12分18、解:(1)图象关于对称即.当时,,...